练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．一队学生从学校出发去部队军训，行进的速度是5km/h，走了4.5km后，一名通讯员按原路返回学校报信，然后追赶队伍，通讯员的速度是14km/h，他在距部队6km处追上了队伍，问学校到部队的路程是多少千米？（报信时间忽略不计）

    分析 先设通讯员从返回到追上队伍用的时间是x小时，根据学生队伍所走的路程=通讯员走的路程减去4.5千米，列出方程，求出x的值，从而求出学校到部队的距离．

    解答 解：设通讯员从返回到追上队伍用的时间是x小时，由题意，得
    4.5+5x=14x-4.5，
    解得：x=1．
    则学校到部队的距离为：4.5+5×1+6=15.5（千米）．
    答：学校到部队的路程是15.5千米．

    点评 本题考查了一元一次方程的应用，用到的知识点是路程=速度×时间，解答时根据学生队伍所走的路程=通讯员走的路程减去学生当时行进的路程，从而列出方程是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    16．一个窗户的形状如图所示，如果窗户的用料是19米，则窗户面积y（m2）与宽x（m）间的函数关系式为y=-x2+6.5x，当边长x为3.25时，室内的光线最充足．（精确到0.1m）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．计算：5$\frac{1}{2}$$-（-\frac{6}{11}）$$-[1-\frac{1}{4}+（-2）^{2}×（-2\frac{2}{3}）+\frac{1}{3}-1-（-\frac{1}{2}）^{2}]$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

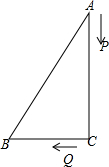    14．如图，Rt△ABC中，∠C=90°，BC=a，AC=b（a＜b），AB=5，a，b是方程x2-（m-1）x+（m+4）=0的两根
    （1）求a，b；
    （2）P，Q两点分别从A，C出发，分别以每秒2个单位，1个单位的速度沿边AC，BC向终点C，B运动，（有一个点达到终点则停止运动），求经过多长时间后PQ=2？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．已知-4ya+3x3与4x3-by4能合并成一项，则代数式b4-6a3b-4b4+2ba3的值是0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．已知（a+b-12）2+|a-b+3|=0，求代数式$\frac{1}{2}$（a-b）+$\frac{1}{4}$（a+b）+$\frac{a+b}{3}$-$\frac{a-b}{6}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

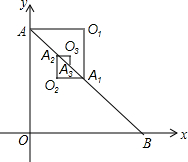    6．如图，在Rt△AOB中，OA=OB=1，取AB的中点A1，以AA1为斜边作等腰直角三角形AO1A1，取AA1的中点A2，以A1A2为斜边作等腰直角三角形A1O2A1；取A1A2的中点A3，以A2A3为斜边作等腰直角三角形A2O3A3…，则点O6的坐标是（$\frac{21}{64}$，$\frac{21}{32}$）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

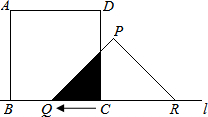    3．如图，有一边长为5cm的正方形ABCD和等腰Rt△PQR，QR=8cm，点B、C、Q、R在同一条直线上，当C、Q两点重合时，△PQR以1cm/秒的速度向左开始匀速运动，设与正方形重合部分的面积为S cm2．
    （1）求S与运动时间t（秒）的函数关系式，并指出自变量的取值范围；
    （2）求S的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

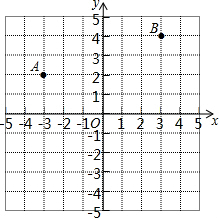    4．已知两点A（-3，2），B（3，4）．
    （1）在如图所示的坐标系中画出点A和点B；
    （2）在x轴上找一点P，使PA+PB最小，并写出P的坐标．

    查看答案和解析>>

    同步练习册答案