
【题目】如图,扇形OAB的半径OA=3,圆心角∠AOB=90°,点C是弧AB上异于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连结DE,点G、H在线段DE上,且DG=GH=HE
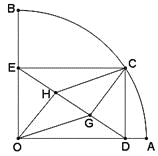
(1)求证:四边形OGCH是平行四边形;
(2)当点C在弧AB上运动时,在CD、CG、DG中,是否存在长度不变的线段?若存在,请求出该线段的长度;
(3)求证:![]() 是定值.
是定值.
【答案】(1)见详解;(2)DG不变;DG=1;(3)见详解.
【解析】
(1)连接OC,容易根据已知条件证明四边形ODCE是矩形,然后利用其对角线互相平分和DG=GH=HE可以知道四边形CHOG的对角线互相平分,从而判定其是平行四边形;
(2)由于四边形ODCE是矩形,而矩形的对角线相等,所以DE=OC,而CO是圆的半径,这样DE的长度不变,也就DG的长度不变;
(3)过C作CN⊥DE于N,设CD=x,然后利用三角形的面积公式和勾股定理用x表示CN,DN,HN,再利用勾股定理就可以求出CD2+3CH2的值了.
(1)连结OC,交DE于M,
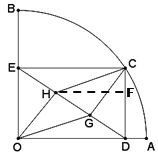
∵四边形ODCE是矩形
∴OM=CM,EM=DM
又∵DG=HE
∴EM-EH=DM-DG,即HM=GM
∴四边形OGCH是平行四边形
(2)DG不变;
在矩形ODCE中,DE=OC=3,所以DG=1
(3)作HF⊥CD于点F,则△DHF∽△DEC
∴![]()
∴![]()
∴![]()
∵HF2=CH2-CF2=DH2-DF2,DH=2
∴CH2-![]() =2-
=2-![]()
整理,得![]()
∴![]() =12
=12


科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点A,B,与
与x轴交于点A,B,与![]() 轴交于点C。过点C作CD∥x轴,交抛物线的对称轴于点D,连结BD。已知点A坐标为(-1,0)。
轴交于点C。过点C作CD∥x轴,交抛物线的对称轴于点D,连结BD。已知点A坐标为(-1,0)。

(1)求该抛物线的解析式;
(2)求梯形COBD的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①b2﹣4ac<0;
②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;
③2a+b=0;
④当y>0时,x的取值范围是﹣1<x<3;
⑤当x>0时,y随x增大而减小.
其中结论正确的个数是( )
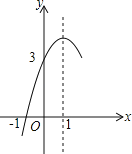
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①已知线段CD所在直线的解析式为y=﹣![]() x+3,分别交坐标轴于点C、D,
x+3,分别交坐标轴于点C、D,
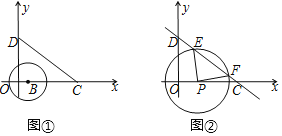
(1)若以点B(1,0)为圆心的⊙B半径为r,⊙B与线段CD只有一个交点,则r满足 .
(2)如图②,如果点P从(﹣5,0)出发,以1个单位长度的速度沿x轴向右作匀速运动,当运动时间到t秒时,以点P为圆心、![]() t个单位长度为半径的圆P与线段CD所在直线有两个交点,分别为点E、F,且∠EPF=2∠OCD,求此时t的值.
t个单位长度为半径的圆P与线段CD所在直线有两个交点,分别为点E、F,且∠EPF=2∠OCD,求此时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家经销一种绿茶,用于装修门面已投资4000元已知绿茶每千克成本40元,经研究发现销量y(kg)与销售单价x(元/kg)之间的函数关系是![]() (
(![]() ).以该绿茶的月销售利润为w(元)[销售利润
).以该绿茶的月销售利润为w(元)[销售利润![]() (每千克单价
(每千克单价![]() 每千克成本)
每千克成本)![]() 销售量]
销售量]
(1)求m与之间的函数关系式,并求出x为何值时,w的值最大?
(2)若在第一个月里,按使w获得最大值的销售单价进行销售后,在第二个月里受物价部门干预,销售单价不得高于85元,要想在全部收回投资的基础上使第二个月的利润达到2200元,那么第二个月里应该确定销售单价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为预防禽流感,上海建立了候鸟监测站,某候鸟监测站将一天7点至17点监测到上空飞过的候鸟数制成了如下直方图:
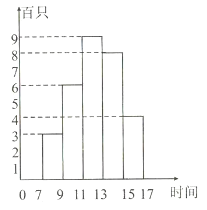
(1)候鸟飞过的高峰期在一天的______;
(2)这一天7点至17点期间,平均每小时飞过上空的候鸟有______只;
(3)每两个小时飞过上空的候鸟数的中位数是______;
(4)若一天飞过上空的候鸟数按此估算,该监测站九月份监测到的候乌只数约是______只;
(5)7时—9时段的频率是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(3,1),B(1,0),PQ是直线y=x上的一条动线段且PQ=![]() (Q在P的下方),当AP+PQ+QB取最小值时,点Q坐标为______.
(Q在P的下方),当AP+PQ+QB取最小值时,点Q坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
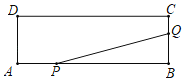
【题目】如图,矩形ABCD的两边长AB=16cm,AD=4cm,点P,Q分别从A,B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动设运动时间为x(秒),设△BPQ的面积为ycm2.
(1)求y关于x的函数关系式,并写出x的取值范围;
(2)当△BPQ面积有最大值时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线![]() 与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.
与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.
(1)求该抛物线的解析式;
(2)如图①,若点D是抛物线上一动点,设点D的横坐标为m(0<m<3),连接CD,BD,BC,AC,当△BCD的面积等于△AOC面积的2倍时,求m的值;
(3)若点N为抛物线对称轴上一点,请在图②中探究抛物线上是否存在点M,使得以B,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点M的坐标;若不存在,请说明理由.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com