练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
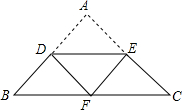
    9．如图，在△ABC中，AB=AC，DE∥BC，现将△ABC沿DE进行折叠，使点A恰好落在BC上的点F处，则△FDE与△ABC的周长比为1：2．

    分析 连接AF，由翻折的性质可知AG=AF=1：2，△FDE的周长=△ADE的周长，由DE∥BC可知△ADE∽△ABC，依据相似三角形的周长之比=相似比=对应高的比求解即可．

    解答 解：如图所示：连接AF．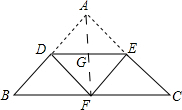

    由翻折的性质可知：AG=GF，AG⊥DE，△FDE的周长=△ADE的周长．
    ∵ED∥BC，
    ∴AF⊥BC．
    ∴$\frac{AD}{AB}=\frac{AG}{AF}$=$\frac{1}{2}$．
    ∵DE∥BC，
    ∴△ADE∽△ABC．
    ∴△FDE与△ABC的周长比为=1：2．
    故答案为：1：2．

    点评 本题主要考查的是翻折的性质、相似三角形的性质和判定、根据翻折的性质求得AD：AB=1：2是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    19．用一根钉子钉木条时，木条用来回晃动，用数学知识说明理由：过一点有无数条直线
    用两根钉子钉木条时，木条会被固定不动，用数学知识说明理由：过两点有且只有一条直线．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．下列事件中是必然事件的是（　　）
    A．平安夜下雪B．地球在自转的同时还不停的公转
    C．所有人15岁时身高必达到1.70米D．下雨时一定打雷

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

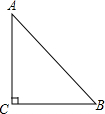    17．如果三角形有一个边上的中线长恰好等于这个边的长，那么称这个三角形是“有趣三角形”，这条中线为“有趣中线”．如图，在△ABC中，∠C=90°，较短的一条直角边BC=1，且△ABC是“有趣三角形”，求△ABC的“有趣中线”的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

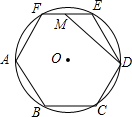    4．如图，正六边形ABCDEF内接于⊙O，M为EF的中点，连接DM，若⊙O的半径为2，则MD的长度为（　　）
    A．$\sqrt{7}$B．$\sqrt{5}$C．2D．1

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．如图，在“妙手推推推”的游戏中，主持人出示了一个9位数，让参加者猜商品价格．被猜的价格是一个4位数，也就是这个9位中从左到右连在一起的某4个数字．如果参与者不知道商品的价格，从这些连在一起的所有4位数中，任意猜一个，求他猜中该商品价格的概率（　　）
    A．$\frac{1}{9}$B．$\frac{1}{6}$C．$\frac{1}{5}$D．$\frac{1}{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．先化简，再求值：$\frac{x-4}{x-3}÷$（x+3-$\frac{7}{x-3}$），其中x=-$\frac{1}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．某市因道路建设需要开挖土石方，计划每小时挖掘土石方540m3，现决定向某租赁公司租用甲、乙两种型号的挖掘机来完成这项工作，租赁公司提供的挖掘机有关信息如下表所示：
    租金（单位：元/台•时）挖掘土石方量（单位：m3/台•时）
    甲型挖掘机12080　
    乙型挖掘机10060
    （1）若租用甲、乙两种型号的挖掘机共8台，恰好完成每小时的挖掘量，则甲、乙两种型号的挖掘机各需多少台？
    （2）如果每小时支付的租金不超过850元，又恰好完成每小时的挖掘量，那么共有哪几种不同的租用方案？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．如果x=6是方程2x+3a=6x的解，那么a的值是（　　）
    A．4B．8C．9D．-8

    查看答案和解析>>

    同步练习册答案