
| 租金(单位:元/台•时) | 挖掘土石方量(单位:m3/台•时) | |
| 甲型挖掘机 | 120 | 80 |
| 乙型挖掘机 | 100 | 60 |
分析 (1)设甲、乙两种型号的挖掘机各需x台、y台,根据甲、乙两种型号的挖掘机共8台和每小时挖掘土石方540m3,列出方程求解即可;
(2)设租用m辆甲型挖掘机,n辆乙型挖掘机,根据题意列出二元一次方程,求出其正整数解;然后分别计算支付租金,选择符合要求的租用方案.
解答 解:设甲、乙两种型号的挖掘机各需x台、y台.
依题意得:$\left\{\begin{array}{l}{x+y=8}\\{80x+60y=540}\end{array}\right.$,
解得 $\left\{\begin{array}{l}{x=3}\\{y=5}\end{array}\right.$.
答:甲、乙两种型号的挖掘机各需3台、5台;
(2)设租用m辆甲型挖掘机,n辆乙型挖掘机.
依题意得:80m+60n=540,化简得:4m+3n=27.
∴n=9-$\frac{4}{3}$m,
∴方程的解为$\left\{\begin{array}{l}{m=3}\\{n=5}\end{array}\right.$或$\left\{\begin{array}{l}{m=6}\\{n=1}\end{array}\right.$.
当m=3,n=5时,支付租金:120×3+100×5=860元>850元,超出限额;
当m=6,n=1时,支付租金:120×6+100×1=820元<850元,符合要求.
答:有一种租车方案,即租用6辆甲型挖掘机和1辆乙型挖掘机.
点评 本题考查了一元一次不等式和二元一次方程组的应用.解决问题的关键是读懂题意,依题意列出等式(或不等式)进行求解.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
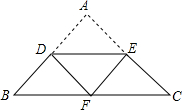 如图,在△ABC中,AB=AC,DE∥BC,现将△ABC沿DE进行折叠,使点A恰好落在BC上的点F处,则△FDE与△ABC的周长比为1:2.
如图,在△ABC中,AB=AC,DE∥BC,现将△ABC沿DE进行折叠,使点A恰好落在BC上的点F处,则△FDE与△ABC的周长比为1:2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一个几何体由几个大小相同的小立方块搭成,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,请画出从正面、左面看到的这个几何体的形状图.
一个几何体由几个大小相同的小立方块搭成,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,请画出从正面、左面看到的这个几何体的形状图.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
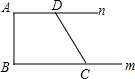 如图所示,已知直线m∥n,点A、D在n上,点B、C在m上,且AB⊥n于点A,∠ADC=120°,若CD=6,则AB的长为3$\sqrt{3}$.
如图所示,已知直线m∥n,点A、D在n上,点B、C在m上,且AB⊥n于点A,∠ADC=120°,若CD=6,则AB的长为3$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
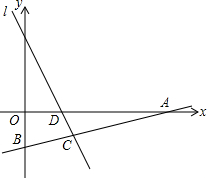 如图,直线l1的解析式为y=-2x+2,且l1与x轴交于点D,直线l2经过点A(4,0),B(0,-1),两直线交于点C.
如图,直线l1的解析式为y=-2x+2,且l1与x轴交于点D,直线l2经过点A(4,0),B(0,-1),两直线交于点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com