
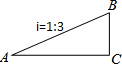
 如图,小明沿坡度i=1:3的一段斜坡从A向上爬行到B,已知AB=30米,则小明在水平方向上前进了9$\sqrt{10}$米.
如图,小明沿坡度i=1:3的一段斜坡从A向上爬行到B,已知AB=30米,则小明在水平方向上前进了9$\sqrt{10}$米.  应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:解答题
| 租金(单位:元/台•时) | 挖掘土石方量(单位:m3/台•时) | |
| 甲型挖掘机 | 120 | 80 |
| 乙型挖掘机 | 100 | 60 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
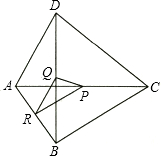 如图,已知四边形ABCD,点P、Q、R分别是对角线AC、BD和边AB的中点,设$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.
如图,已知四边形ABCD,点P、Q、R分别是对角线AC、BD和边AB的中点,设$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
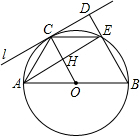 如图,⊙O的直径AB,C为圆周上一点,过点C作⊙O的切线l,过点B作l的垂线BD,垂足为D,BD与⊙O交于点E,连接EA、EC.若AB=4,AC=2,则ED的长1.
如图,⊙O的直径AB,C为圆周上一点,过点C作⊙O的切线l,过点B作l的垂线BD,垂足为D,BD与⊙O交于点E,连接EA、EC.若AB=4,AC=2,则ED的长1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
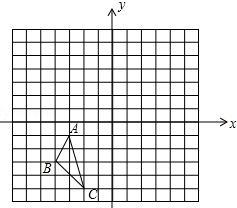 如图,△ABC三个顶点的坐标分别为A(-3,-1)、B(-4,-3)、C(-2,-5).
如图,△ABC三个顶点的坐标分别为A(-3,-1)、B(-4,-3)、C(-2,-5).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知△ABC中,AC=BC,∠ACB=90°,D,E分别为AB,BC上一点,连接DE.
已知△ABC中,AC=BC,∠ACB=90°,D,E分别为AB,BC上一点,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
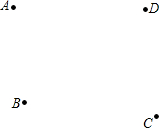 如图,已知A,B,C,D四个点.
如图,已知A,B,C,D四个点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com