
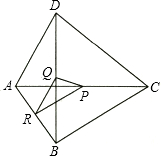
 如图,已知四边形ABCD,点P、Q、R分别是对角线AC、BD和边AB的中点,设$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.
如图,已知四边形ABCD,点P、Q、R分别是对角线AC、BD和边AB的中点,设$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.分析 (1)由点P、Q、R分别是对角线AC、BD和边AB的中点,直接利用三角形中位线的性质,即可求得$\overrightarrow{PR}$=$\frac{1}{2}$$\overrightarrow{CB}$=-$\frac{1}{2}$$\overrightarrow{a}$,$\overrightarrow{RQ}$=$\frac{1}{2}$$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{b}$,再利用三角形法则求解即可求得答案;
(2)利用平行线四边形法则求解即可求得答案.
解答  解:(1)∵点P、Q、R分别是对角线AC、BD和边AB的中点,
解:(1)∵点P、Q、R分别是对角线AC、BD和边AB的中点,
∴$\overrightarrow{PR}$=$\frac{1}{2}$$\overrightarrow{CB}$=-$\frac{1}{2}$$\overrightarrow{a}$,$\overrightarrow{RQ}$=$\frac{1}{2}$$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{b}$,
∴$\overrightarrow{PQ}$=$\overrightarrow{PR}$+$\overrightarrow{RQ}$=-$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$;
(2)如图:$\overrightarrow{PR}$与$\overrightarrow{PE}$即为所求.
点评 此题考查了平行向量的知识.注意掌握三角形法则与平行四边形法则的应用.


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:解答题
 一个几何体由几个大小相同的小立方块搭成,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,请画出从正面、左面看到的这个几何体的形状图.
一个几何体由几个大小相同的小立方块搭成,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,请画出从正面、左面看到的这个几何体的形状图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
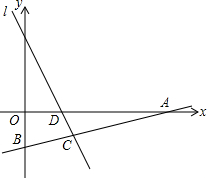 如图,直线l1的解析式为y=-2x+2,且l1与x轴交于点D,直线l2经过点A(4,0),B(0,-1),两直线交于点C.
如图,直线l1的解析式为y=-2x+2,且l1与x轴交于点D,直线l2经过点A(4,0),B(0,-1),两直线交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
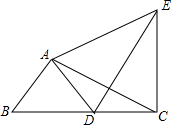 如图,在Rt△ABC中,∠BAC=90°,AB=3,cosB=$\frac{3}{5}$,将△ABC绕着点A旋转得△ADE,点B的对应点D落在边BC上,联结CE,那么CE的长是$\frac{24}{5}$.
如图,在Rt△ABC中,∠BAC=90°,AB=3,cosB=$\frac{3}{5}$,将△ABC绕着点A旋转得△ADE,点B的对应点D落在边BC上,联结CE,那么CE的长是$\frac{24}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
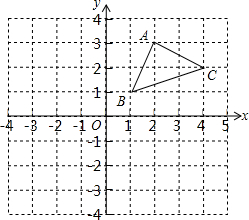 如图,在平面直角坐标系中有三个点A(2,3),B(1,1),C(4,2).
如图,在平面直角坐标系中有三个点A(2,3),B(1,1),C(4,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,数轴上点A对应的数为a,点B对应的数为b,且a、b满足|2a+6|+3(b-2)2=0,
如图,数轴上点A对应的数为a,点B对应的数为b,且a、b满足|2a+6|+3(b-2)2=0,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在正方形网格中建立如图所示的平面直角坐标系xOy,△ABC的三个顶点都在格点上,点A的坐标是(4,4),请解答下列问题:
在正方形网格中建立如图所示的平面直角坐标系xOy,△ABC的三个顶点都在格点上,点A的坐标是(4,4),请解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com