
����Ŀ���ڽ������Ĵ����ڼ䣬���ŵĹ滮ѡ���뾭���л�������Ҽ���Ȼ������---����A������B��Ϊʵ�ְ����������������������Ŀ�꣬���������ʩ��ʱ��͵ص㣬Ϊ�ˣ�����۲�Ա����ͬ��������������20�죬������A��B���ض��л�������ټ������˹۲��ͳ�ƣ��������£��벹������������λ��ͷ��
���ռ����ݣ�
����20��۲첻ͬ�л�����ÿ��������A������B���ֵ���Ŀ������õ�ͳ�ƽ����������С�����˳���������£�
����A 0 1 3 4 5 6 6 6 7 8 8 9 11 14 15 15 17 23 25 30
B 1 1 3 4 6 6 89 11 12 14 15 16 16 16 17 22 25 26 35
���������������ݣ�
��1�������������������������������ݣ��벹��������
������x | 0��x��7 | 8��x��14 | 15��x��21 | 22��x��28 | 29��x��35 |
����A | 9 | 5 | 3 | ______ | ______ |
����B | 6 | 5 | 5 | 3 | 1 |
��2���������ݵļ��ƽ��������λ�����������±���ʾ
�۲�� | ���� | ƽ���� | ��λ�� | ���� |
����A | a | 10.65 | b | c |
����B | 34 | 13.15 | 13 | 16 |
����գ��ϱ��У�����a=______����λ��b=______������c=______��
��3���滮����ѡ��������AΪ���ŵıؾ��أ�Ϊ����ʩ�������Ӱ�죬��������ʩ��ʱ�䣬�����ڽ�������200��ʩ�����ڣ�����A��Լ�ж������л�������ֵ���Ŀ��22��x��35�ķ�Χ�ڣ�
���𰸡���1��2��1����2��30��8��6����3��22��x��35.
��������
��1��������Ŀ�е����ݣ����Խ�����������
��2��������Ŀ�е����ݿ��Էֱ����a��b��c��ֵ��
��3�����������������壬���ϱ����е����ݿ����������A��Լ�ж������л�������ֵ���Ŀ��22��x��35�ķ�Χ�ڣ�
�⣺��1�����ռ������е����ݿɵã�
22��x��28ʱ���л�����������A���ֵ���ĿΪ��2��
29��x��35ʱ���л�����������A���ֵ���ĿΪ��1��
�ʴ�Ϊ��2��1��
��2�����ռ������е����ݿɵã�
a=30-0=30��b=8��c=6��
�ʴ�Ϊ��30��8��6��
��3��200��![]() =30���죩��
=30���죩��
������A��Լ��30���л�������ֵ���Ŀ��22��x��35�ķ�Χ�ڣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�ڣ�����y��![]() ��ͼ���뷴��������y��
��ͼ���뷴��������y��![]() ��k��0��ͼ���й�����A����A������Ϊ��8��a����AB��x�ᣬ����Ϊ��B��
��k��0��ͼ���й�����A����A������Ϊ��8��a����AB��x�ᣬ����Ϊ��B��
��1�����������Ľ���ʽ��
��2����P���߶�OB�ϣ���AP��BP+2�����߶�OP�ij���
��3����DΪ����OA��һ�㣬�ڣ�2���������£���S��ODP��S��ABO�����D�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ɽ�����г�Խ��Խ�ܵ���ѧ����ϲ��������Ʒ�����Ͷ���г���ij���о�Ӫ��A�ͳ�ȥ�������ܶ�Ϊ50000Ԫ�����������ܶ��ȥ�����20%��ÿ�����ۼ۱�ȥ�꽵��400Ԫ����������������������ͬ��A��B�����ͺų�����Ľ��������ۼ۸����
A�ͳ� | B�ͳ� | |
�����۸�Ԫ�� | 1100 | 1400 |
���ۼ۸�Ԫ�� | ��������ۼ۸� | 2000 |
��1�������A�ͳ�ÿ���ۼ۶���Ԫ��
��2���ó��мƻ��½�һ��A�ͳ����¿�B�ͳ���60������B�ͳ��Ľ�������������A�ͳ���������������������������õ���������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڼס������������IJ������״���װ��3����ȫ��ͬ��С�ֱ��������0��1��2���Ҵ���װ��3����ȫ��ͬ��С�ֱ����������1����2��0���ִӼ״��������ȡһ��С��¼���е�����Ϊx���ٴ��Ҵ��������ȡһ��С��¼���е�����Ϊy��ȷ����M����Ϊ��x��y����
��1������״ͼ���б����оٵ�M���п��ܵ����ꣻ
��2�����M��x��y���ں���y=-x+1��ͼ���ϵĸ��ʣ�
��3����ƽ��ֱ������ϵxOy�У���O�İ뾶��2�������M��x��y��������O�����ߵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������κ���y=-��x-2��2+4��x��4����ͼ����ֱ��x=4���ۣ�����ǰ���ͼ�����һ����ͼ��M����ֱ��y=b��ͼ��M���ĸ����㣬���ͼ���֪��b��ȡֵ��Χ��______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
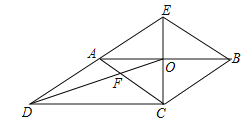
����Ŀ����ͼ��CE��ABCD�ı�AB�Ĵ�ֱƽ���ߣ�����Ϊ��O��CE��DA���ӳ��߽��ڵ�E������AC��BE��DO��DO��AC���ڵ�F�������н��ۣ�
���ı���ACBE�����Σ�
�ڡ�ACD����BAE��
��AF��BE��2��3��
��S�ı���AFOE��S��COD��2��3��
������ȷ�Ľ�����_____������д������ȷ���۵���ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��С��ͬѧ�����Ƶ�ֱ��������ֽ��DEF������AB�ĸ߶ȣ��������Լ���λ�ã��跨ʹб��DF����ˮƽ�����ұ�DE���B��ͬһֱ���ϣ���ֽ֪�������ֱ�DZ�DE��40cm��EF��20cm����ñ�DF�����ĸ߶�AC��1.5m��CD��8m������AB�ĸ߶ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������MNOK����������ABCDEF�߳���Ϊ1���������η������������У�ʹOK����AB���غϣ���ͼ��ʾ�������в�����������������������������Ƶ�B˳ʱ����ת��ʹKM����BC���غϣ���ɵ�һ����ת�����Ƶ�C˳ʱ����ת��ʹMN����CD���غϣ���ɵڶ�����ת������������������ת������ת�Ĺ����У��������κ��������εı��غ�ʱ����B��M��ľ�������ǣ�������
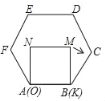
A. 0.5B. 0.7C. ![]() ��1D.
��1D. ![]() ��1
��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����ÿ��5�¶�����������ڻ�������ʽ��A�����衢B�����衢C���滭��D���ݽ�������ʽ��ѧУΧ�ơ�����ϲ���Ļ��ʽ��ʲô�����ڰ��꼶ѧ���н�������������飨�ĸ�ѡ���б�����ֻѡһ������ݵ���ͳ�ƽ������������ͼ���ֲ�������ͳ��ͼ����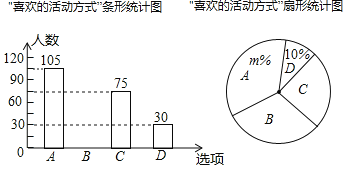
����ͳ��ͼ�����ش��������⣺
��1�����γ���ѧ����300�ˣ�m=35����������ͳ��ͼ����������
��2��ѧУ���ó�ǩ��ʽ��ÿ����A��B��C��D�������չʾ��������״ͼ���б�����ij�����鵽�����ʽǡ���ǡ����衱�͡��赸���ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com