
如图1,已知梯形OABC,抛物线分别过点O(0,0)、A(2,0)、B(6,3).
(1)直接写出抛物线的对称轴、解析式及顶点M的坐标;
(2)将图1中梯形OABC的上下底边所在的直线OA、CB以相同的速度同时向上平移,分别交抛物线于点O1、A1、C1、B1,得到如图2的梯形O1A1B1C1.设梯形O1A1B1C1的面积为S,A1、 B1的坐标分别为 (x1,y1)、(x2,y2).用含S的代数式表示x2-x1,并求出当S=36时点A1的坐标;
(3)在图1中,设点D的坐标为(1,3),动点P从点B出发,以每秒1个单位长度的速度沿着线段BC运动,动点Q从点D出发,以与点P相同的速度沿着线段DM运动.P、Q两点同时出发,当点Q到达点M时,P、Q两点同时停止运动.设P、Q两点的运动时间为t,是否存在某一时刻t,使得直线PQ、直线AB、x轴围成的三角形与直线PQ、直线AB、抛物线的对称轴围成的三角形相似?若存在,请求出t的值;若不存在,请说明理由.


(1)对称轴:直线x=1,解析式:y= x2-
x2-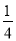 x,顶点坐标:M(1,-
x,顶点坐标:M(1,- ).(2) A1(6,3).(3) t=
).(2) A1(6,3).(3) t=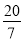 .
.
【解析】
试题分析:(1)已知了O、A、B的坐标,可用待定系数法求出抛物线的解析式,进而可得到其对称轴方程和顶点M的坐标.
(2)在两条直线平移的过程中,梯形的上下底发生了改变,但是梯形的高没有变化,仍为3,即y2-y1=3,可根据抛物线的解析式,用x1、x2表示出y1、y2,然后联立y2-y1=3,可得到第一个关于x1、x2的关系式①;在两条直线平移过程中,抛物线的对称轴没有变化,可用x1、x2以及抛物线的对称轴解析式表示出梯形上下底的长,进而可得到梯形面积的表达式,这样可得到另外一个x1、x2的关系式②,联立两个关系式,即可得到关于(x2-x1)与S的关系式③,将S=36代入②③的关系式中,即可列方程组求得x1、x2的值,进而可求出A点的坐标.
(3)要解答此题,首先要弄清几个关键点:
一、当PQ∥AB时,设直线AB与抛物线对称轴的交点为E,可得△DPQ∽△DBE,可用t表示出DP、DQ的长,而E点坐标易求得,根据相似三角形所得比例线段,即可得到此时t的值即t=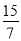 ;
;
二、当P、Q都停止运动时,显然BC>DM,所以此时t=DM÷1=3 ;可分两种情况讨论:
;可分两种情况讨论:
①当0<t<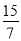 时,设直线PQ与直线AB的交点为F,与x轴的交点为G;由题意知△FQE∽△FAG,得∠FGA=∠FEQ,由于BC∥x轴,则∠DPQ=∠FGA=∠FEQ,由此可证得△DPQ∽△DEB,DB、DE的长已求得,可用t表示出DP、DQ的长,根据相似三角形所得比例线段,即可求得此时t的值;
时,设直线PQ与直线AB的交点为F,与x轴的交点为G;由题意知△FQE∽△FAG,得∠FGA=∠FEQ,由于BC∥x轴,则∠DPQ=∠FGA=∠FEQ,由此可证得△DPQ∽△DEB,DB、DE的长已求得,可用t表示出DP、DQ的长,根据相似三角形所得比例线段,即可求得此时t的值;
②当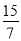 <t<3
<t<3 时,方法同①;
时,方法同①;
在求得t的值后,还要根据各自的取值范围将不合题意的解舍去.
试题解析::(1)对称轴:直线x=1,
解析式:y= x2-
x2-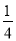 x,
x,
顶点坐标:M(1,- ).
).
(2)由题意得y2-y1=3,y2-y1= x22-
x22-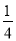 x2-
x2- x12+
x12+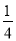 x1=3,
x1=3,
得:(x2-x1)[ (x2+x1)-
(x2+x1)-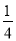 ]=3①,
]=3①,
s=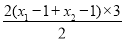 =3(x1+x2)-6,
=3(x1+x2)-6,
得:x1+x2=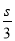 +2②,
+2②,
把②代入①并整理得:x2-x1=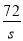 (S>0),
(S>0),
当s=36时, ,
,
解得: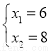 ,
,
把x1=6代入抛物线解析式得y1=3,
∴点A1(6,3).
(3)存在
易知直线AB的解析式为y= x-
x-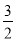 ,可得直线AB与对称轴的交点E的坐标为(1,-
,可得直线AB与对称轴的交点E的坐标为(1,- ),
),
∴BD=5,DE=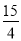 ,DP=5-t,DQ=t,
,DP=5-t,DQ=t,
当PQ∥AB时,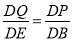 ,即
,即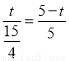 ,
,
得t=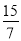 ,
,
下面分两种情况讨论:设直线PQ与直线AB、x轴的交点分别为点F、G;
当0<t<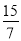 时,如图1-1;
时,如图1-1;
∵△FQE∽△FAG,∴∠FGA=∠FEQ,
∴∠DPQ=∠DEB;易得△DPQ∽△DEB,
∴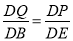 ,
,
∴ ,
,
得t=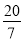 >
>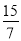 ,
,
∴t=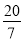 (舍去);
(舍去);
当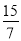 <t<3
<t<3 时,如图1-2;
时,如图1-2;
∵△FQE∽△FAG,
∴∠FAG=∠FQE,
∵∠DQP=∠FQE,∠FAG=∠EBD,
∴∠DQP=∠DBE,易得△DPQ∽△DEB,
∴
∴ ,
,
∴t=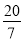 ;
;
∴当t=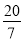 秒时,使直线PQ、直线AB、x轴围成的三角形与直线PQ、直线AB、抛物线的对称轴围成的三角形相似.
秒时,使直线PQ、直线AB、x轴围成的三角形与直线PQ、直线AB、抛物线的对称轴围成的三角形相似.

考点:二次函数综合题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2013-2014学年山东省济南市长清区九年级复习调查考试(一模)数学试卷(解析版) 题型:选择题
如图,双曲线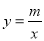 与直线
与直线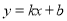 交于点M、N,并且点M的坐标为(1,3),点N的纵坐标为-1.根据图象信息可得关于x的方程
交于点M、N,并且点M的坐标为(1,3),点N的纵坐标为-1.根据图象信息可得关于x的方程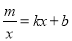 的解为
的解为
A.-3,1 B.-3,3 C.-1,1 D.-1,3
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省济南市九年级中考模拟数学试卷(解析版) 题型:选择题
如果+30m表示向东走30m,那么向西走40m表示为( )
A.+40m B.-40m C.+30m D.-30m
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省九年级第一次学业水平模拟考试数学试卷(解析版) 题型:选择题
在同一直角坐标系下,直线y=x+1与双曲线 的交点的个数为( )
的交点的个数为( )
(A)0个 (B)1个 (C)2个 (D)不能确定
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省九年级第一次学业水平模拟考试数学试卷(解析版) 题型:选择题
如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠1=25°,则∠2的度数为( )
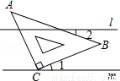
(A)20° (B)25° (C)30° (D) 35°
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省泰安市九年级学业模拟考试数学试卷(解析版) 题型:填空题
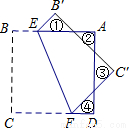
如图,正方形纸片ABCD的边长为8,将其沿EF折叠,则图中①②③④四个三角形的周长之和为
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省泰安市九年级学业模拟考试数学试卷(解析版) 题型:选择题
据统计,今年泰安市中考报名确认考生人数是96 200人,用科学记数法表示96 200为
A.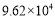 B.
B. 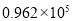 C.
C.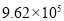 D.
D.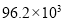
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省德州市九年级第一次模拟考试数学试卷(解析版) 题型:解答题
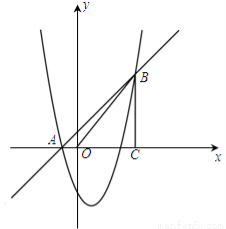
如图,已知抛物线y=x2+bx+c经过A(-1, 0)、B(4, 5)两点,过点B作BC⊥x轴,垂足为C.
(1)求抛物线的解析式;
(2)求tan∠ABO的值;
(3)点M是抛物线上的一个点,直线MN平行于y轴交直线AB于N,如果以M、N、B、C为顶点的四边形是平行四边形,求出点M的横坐标.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省德州市中考一模数学试卷(解析版) 题型:选择题
下列命题中,正确的是( )
A.平分弦的直径垂直于弦
B.对角线相等的平行四边形是正方形
C.对角线互相垂直的四边形是菱形
D.三角形的一条中线能将三角形分成面积相等的两部分
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com