练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．三边长a，b、c满足a+b=10，ab=18，c=8的三角形是直角三角形（形状）．

    分析 对原式进行变形，发现三边的关系符合勾股定理的逆定理，从而可判定其形状．

    解答 解：∵（a+b）2-2ab
    =100-36
    =64，
    c2=64，
    ∴a2+b2=c2，
    ∴此三角形是直角三角形．
    故答案为：直角三角形．

    点评 此题考查了勾股定理的逆定理，解答此题要用到勾股定理的逆定理：已知三角形ABC的三边满足a2+b2=c2，则三角形ABC是直角三角形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    10．抛物线y=ax2+bx+c上部分点的横坐标x纵坐标y的对应值如下表，则下列说法中错误的是（　　）
    x…-4-3-2-101…
    y…-37-21-9-133…
    A．当x＞1时，y随x的增大而增大
    B．抛物线的对称轴为$x=\frac{1}{2}$
    C．当x=2时，y=-1
    D．方程ax2+bx+c=0一个负数解x1满足-1＜x1＜0

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

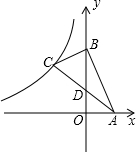    11．如图所示，直线y=-3x+6交x轴、y轴于A、B两点，BC⊥AB，且D为AC的中点，双曲线y=$\frac{k}{x}$过点C，则k=-$\frac{32}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．$a÷\frac{a}{b}•\frac{1}{a}$=$\frac{b}{a}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．已知a、b、c为△ABC的三边，且满足（a-b）（a2+b2-c2）=0，则△ABC是（　　）
    A．等边三角形B．直角三角形
    C．等腰直角三角形D．等腰三角形或直角三角形

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．下列二次根式中，最简二次根式是（　　）
    A．$\sqrt{9x}$B．$\sqrt{x-2}$C．$\sqrt{\frac{x-y}{x}}$D．$\sqrt{3{a}^{2}b}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

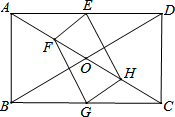    12．已知，在矩形ABCD中，对角线AC、BD相交于点O，E、F、G、H分别是AD、OA、BC、OC的中点．
    （1）求证：四边形EFGH为平行四边形；
    （2）当BC=$\sqrt{3}$AB时，判断四边形EFGH为何种特殊四边形，并证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．在开会前，工作人员进行会场布置，如图为工作人员在主席台上由两人拉着一条绳子，然后以“准绳”摆放整齐的茶杯，这样做的理由是（　　）
    A．两点之间线段最短B．两点确定一条直线
    C．垂线段最短D．过一点可以作无数条直线

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

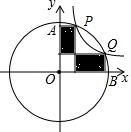    10．如图，点P（2，6）是函数y=$\frac{k}{x}$（k≠0）图象上的一点，以OP为半径作扇形OAB，交y轴于点A，交x轴于点B，且与函数y=$\frac{k}{x}$（k≠0）图象交于点Q．从点P，Q分别向x轴，y轴作垂线，则图中阴影部分的面积是16．

    查看答案和解析>>

    同步练习册答案