
【题目】如图,在ABCD中,点E是AD的中点,延长BC到点F,使CF:BC=1:2,连接DF,EC.若AB=5,AD=8,sinB= ![]() ,则DF的长等于( )
,则DF的长等于( ) 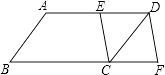
A.![]()
B.![]()
C.![]()
D.2 ![]()
【答案】C
【解析】证明:如图,在ABCD中,∠B=∠ADC,AB=CD=5,AD∥BC,且AD=BC=8. ∵E是AD的中点,
∴DE= ![]() AD.
AD.
又∵CF:BC=1:2,
∴DE=CF,且DE∥CF,
∴四边形CFDE是平行四边形.
∴CE=DF.
过点C作CH⊥AD于点H.
又∵sinB= ![]() ,
,
∴sin∠CDH= ![]() =
= ![]() =
= ![]() ,
,
∴CH=4.
在Rt△CDH中,由勾股定理得到:DH= ![]() =3,则EH=4﹣3=1,
=3,则EH=4﹣3=1,
∴在Rt△CEH中,由勾股定理得到:EC= ![]() =
= ![]() =
= ![]() ,
,
则DF=EC= ![]() .
.
故选:C.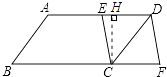
【考点精析】本题主要考查了勾股定理的概念和平行四边形的判定与性质的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,直线l1的解析表达式为y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2,交于点C.
(1)求点D的坐标;
(2)求直线l2的解析表达式;
(3)求△ADC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两个工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用火柴棒按下列方式搭三角形:

(1)填写下面表
三角形个数 | 1 | 2 | 3 | 4 | … |
火柴棒根数 | … |
(2)搭10个这样的三角形需要 根火柴棒.
(3)搭n个这样的三角形需要 根火柴棒.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)在一次数学考试中,从某班随机抽取的10名学生得分(单位:分)如下:75,85,90,90,95,85,95,95,100,98.
(1)求这10名学生得分的众数、中位数和平均数;
(2)若该班共有40名学生,估计此次考试的平均成绩约为多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解学校开展“孝敬父母,从家务劳动做起”活动的实施情况,该校抽取八年级![]() 名学生,调查他们一周(按七天计算)做家务所用时间(单位:小时)得到一组数据,绘制成下表:
名学生,调查他们一周(按七天计算)做家务所用时间(单位:小时)得到一组数据,绘制成下表:
时间 | 划记 | 人数 | 所占百分比 |
|
|
|
|
| 正正正 |
|
|
| 正正 |
| |
| 正 |
|
|
| 正 |
|
|
| 正 |
| |
| 正 |
| |
合计 |
|
|
(1)请填表中未完成的部分;
(2)根据以上信息判断,每周做家务的时间不超过![]() 小时的学生所占的百分比是多少?
小时的学生所占的百分比是多少?
(3)针对以上情况,写出一个20字以内的倡导“孝敬父母,热爱劳动”的句子.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)在上学期的几次测试中,小张和小王的几次数学成绩(单位:分)如下表:

两人都说自己的数学成绩更好.请你想一想:
(1)小张可能是根据什么来判断的?小王可能是根据什么来判断的?
(2)你能根据小张的想法设计一种方案使小张的成绩比小王的高吗?写出你的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读题:课本上有这样一道例题:“解方程:![]()
解:去分母得:
6(x+15)=15-10(x-7)①
6x+90=15-10x+70②
16x=-5③
x=-![]() ④
④
请回答下列问题:
(1)得到①式的依据是________;
(2)得到②式的依据是________;
(3)得到③式的依据是________;
(4)得到④式的依据是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,DE=CE,连接AE并延长交BC的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若AB=2BC,∠F=36°,求∠B的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com