
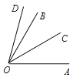
【题目】如图,∠COD=45°,∠BOD=![]() ∠COD,OC是∠AOB的平分线,求∠AOD的度数.
∠COD,OC是∠AOB的平分线,求∠AOD的度数.
【答案】75°.
【解析】
解法一:先根据∠COD=45°,∠BOD=![]() ∠COD求出∠BOD,∠COB的度数,再利用角平分线可求出∠AOB,最后利用∠AOD=∠BOD+∠AOB即可求解.
∠COD求出∠BOD,∠COB的度数,再利用角平分线可求出∠AOB,最后利用∠AOD=∠BOD+∠AOB即可求解.
解法二:先根据∠COD=45°,∠BOD=![]() ∠COD求出∠BOD,∠COB的度数,再利用角平分线可求出∠AOC的度数,最后利用∠AOD=∠COD+∠AOC即可求解.
∠COD求出∠BOD,∠COB的度数,再利用角平分线可求出∠AOC的度数,最后利用∠AOD=∠COD+∠AOC即可求解.
解法一:∵∠COD=45°,∠BOD=![]() ∠COD,
∠COD,
∴∠BOD=![]() ×45° =15°.
×45° =15°.
∴∠COB=∠COD-∠BOD=45°-15°=30°.
∵OC是∠AOB的平分线,
∴∠AOB=2∠COB=2×30°=60°
∴∠AOD=∠BOD+∠AOB=15°+60°=75°.
解法二:∵∠COD=45°,∠BOD=![]() ∠COD,
∠COD,
∴∠BOD=![]() ×45° =15°.
×45° =15°.
∴∠COB=∠COD-∠BOD=45°-15°=30°.
∵OC是∠AOB的平分线,
∴∠AOC=∠COB=30°
∴∠AOD=∠COD+∠AOC=45°+30°=75°


科目:初中数学 来源: 题型:
【题目】(1)如图1,数轴上表示1、![]() 的对应点分别为A、B,点C在OA上,且AC=AB,试求点C所表示的实数.
的对应点分别为A、B,点C在OA上,且AC=AB,试求点C所表示的实数.

(2)如图2,数轴的正半轴上有A、B、C三点,表示1和![]() 的对应点分别为A、B,点B到点A的距离与点C到点O的距离相等,设点C所表示的数为x.求(x﹣
的对应点分别为A、B,点B到点A的距离与点C到点O的距离相等,设点C所表示的数为x.求(x﹣![]() )2的立方根.
)2的立方根.
(3)如图3,a,b,c是数轴上三个点A、B、C所对应的实数.(|c|>|b|>|a|),试化简:![]()
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件中,能判定四边形ABCD为平行四边形的个数是( )
①AB∥CD,AD=BC ; ②AB=CD,AD=BC;③∠A=∠B,∠C=∠D; ④AB=AD,CB=CD.
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察算式:1×3+1=4=22;2×4+1=9=32;3×5+1=16=42;4×6+1=25=52,…
(1)请根据你发现的规律填空:6×8+1=( )2;
(2)用含n的等式表示上面的规律: ;
(3)用找到的规律解决下面的问题:
计算:(1+![]() )(1+
)(1+![]() )(1+
)(1+![]() )(1+
)(1+![]() )…(1+
)…(1+![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长方形纸片ABCD的两条边AB、BC的长度分别为![]() 、
、![]()
![]() ,小明它沿对角线AC剪开,得到两张三角形纸片(如图2),再将这两张三角纸片摆成如图3的形状,点A、B、D、E在同一条直线上,且点B与点D重合,点B、F、C也在同一条直线上.
,小明它沿对角线AC剪开,得到两张三角形纸片(如图2),再将这两张三角纸片摆成如图3的形状,点A、B、D、E在同一条直线上,且点B与点D重合,点B、F、C也在同一条直线上.
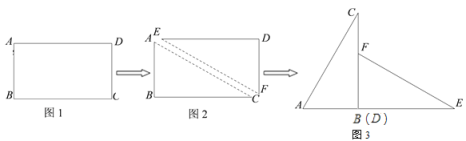
(1)将图3中的△ABC沿射线AE方向平移,使点B与点E重合,点A、C分别对应点M、N,按要求画出图形,并直接写出平移的距离;(用含![]() 或
或![]() 的代数式表示)
的代数式表示)
(2)将图3中的△DEF绕点B逆时针方向旋转60°,点E、F分别对应点P、Q,按要求画出图形,并直接写出∠ABQ的度数;
(3)将图3中的△ABC沿BC所在直线翻折,点A落在点G处,按要求画出图形,并直接写出GE的长度.(用含![]() 、
、![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
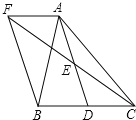
【题目】如图,在![]() 中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且
中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且![]() ,连接BF.
,连接BF.
![]() 证明:
证明:![]() ;
;
![]() 当
当![]() 满足什么条件时,四边形AFBD是矩形?并说明理由.
满足什么条件时,四边形AFBD是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
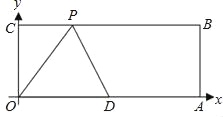
【题目】已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,O为坐标原点,已知直线![]() 经过点A(-6,0),它与y轴交于点B,点B在y轴正半轴上,且OA=2OB
经过点A(-6,0),它与y轴交于点B,点B在y轴正半轴上,且OA=2OB
(1)求直线![]() 的函数解析式
的函数解析式
(2)若直线![]() 也经过点A(-6,0),且与y轴交于点C,如果ΔABC的面积为6,求C点的坐标
也经过点A(-6,0),且与y轴交于点C,如果ΔABC的面积为6,求C点的坐标

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018(第七届)绵阳之春国际车展将于2018年4月18日-22日在绵阳国际会展中心盛大举行。某品牌汽车为了推广宣传,特举行“趣味答题闯关赢大奖”活动,参与者需连续闯过三关方能获得终极大奖。已知闯过第一关的概率为0.8,连续闯过两关的概率为0.5,连续闯过三关的概率为0.3,已经连续闯过两关的参与者获得终极大奖的概率为 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com