
【题目】郑州市采暖季出现 PM2.5 污染,小明妈妈收集了一个月(30 天)的 PM2.5 污染指数,记录如下:(单位:μg/m3)说明:0-50 优,51-100 良,101-150 轻度污染,151-200 中度污染,201-250 重度污染,251 以上严重污染.117,171,170, 208,192,120,243,256,56,115,166,155,156,187,114,49,55, 95,148,160,15,31,62,174,183,162,131,112,96,71对这 30 个数据按组距 50 进行分组,并统计整理,绘制了如下尚不完整的统计图表:
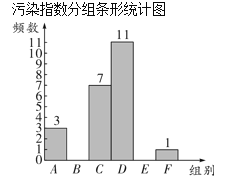
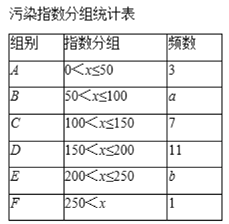
(1)填空:a= ,b= ;
(2)补全频数分布直方图;
(3)这 30 天 PM2.5 污染指数的中位数落在 组;
(4)若一个采暖季为 120 天,请估计空气污染指数不低于 100 的天数(结果取整数)
【答案】(1)6;2;(2)见详解;(3)C;(4)84天.
【解析】
(1)根据题意,找出B组51-100 良的频数,得到a的值,然后利用总数减去其余各组的频数即可得到b的值;
(2)根据频数分布表,即可画出直方图;
(3)根据中位数的定义,这30天的污染指数的中位数落在第15个和第16个数之间,即可得到中位数的位置;
(4)先求出30天中空气污染指数不低于100的百分比,然后计算采暖季空气污染指数不低于100的天数.
解:(1)根据题意,得
这一组数据中,在B组51-100 良的有:56、55、95、62、96、71,共6天;
∴![]() ;
;
∴![]() ;
;
故答案为:6;2.
(2)补全条形图如下:
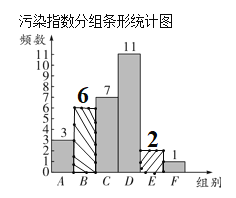
(3)由(2)的条形图可知,
把这30个数据按从小到大排列,第15个数落在C组,第16个数也落在C组,
∴这 30 天PM2.5污染指数的中位数落在C组;
故答案为:C.
(4)根据题意,这30天中空气污染指数不低于100的百分比为:
![]() ,
,
∴在采暖季,空气污染指数不低于100的天数为:
![]() (天).
(天).


科目:初中数学 来源: 题型:
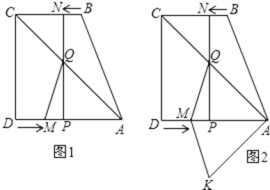
【题目】如图1,直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=8,BC=6,点M从点D出发,以每秒2个单位长度的速度向点A运动,同时,点N从点B出发,以每秒1个单位长度的速度向点C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP⊥AD于点P,连接AC交NP于点Q,连接MQ.设运动时间为t秒.
(1)AM= ,AP= .(用含t的代数式表示)
(2)当四边形ANCP为平行四边形时,求t的值
(3)如图2,将△AQM沿AD翻折,得△AKM,是否存在某时刻t,
①使四边形AQMK为为菱形,若存在,求出t的值;若不存在,请说明理由
②使四边形AQMK为正方形,求 出AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,是由一些棱长为单位1的相同的小正方体组合成的简单几何体.
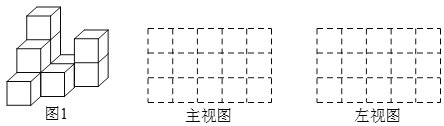
(1)图中有 个小正方体;
(2)请在图1右侧方格中分别画出几何体的主视图、左视图;
(3)不改变(2)中所画的主视图和左视图,最多还能在图1中添加 个小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,△OAB的三个顶点O(0,0)、A(4,1)、B(4,4)均在格点上.
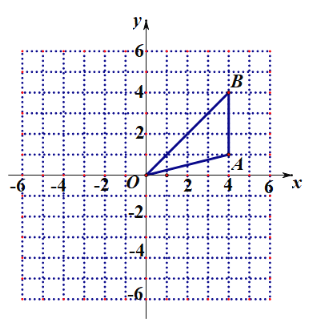
(1)画出△OAB绕原点![]() 顺时针旋转
顺时针旋转![]() 后得到的△
后得到的△![]() ,并写出点
,并写出点![]() 的坐标;
的坐标;
(2)在(1)的条件下,求线段![]() 在旋转过程中扫过的扇形的面积.
在旋转过程中扫过的扇形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学分别进行6次射击训练,训练成绩(单位:环)如下表
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六交 | |
甲 | 9 | 8 | 6 | 7 | 8 | 10 |
乙 | 8 | 7 | 9 | 7 | 8 | 8 |
对他们的训练成绩作如下分析,其中说法正确的是( )
A. 他们训练成绩的平均数相同 B. 他们训练成绩的中位数不同
C. 他们训练成绩的众数不同 D. 他们训练成绩的方差不同
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线![]() 经过点
经过点![]() 和点
和点![]() .
.
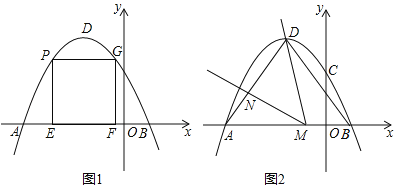
(1)求抛物线的解析式及顶点![]() 的坐标;
的坐标;
(2)点![]() 是抛物线上
是抛物线上![]() 、
、![]() 之间的一点,过点
之间的一点,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,当矩形
,当矩形![]() 的周长最大时,求点
的周长最大时,求点![]() 的横坐标;
的横坐标;
(3)如图2,连接![]() 、
、![]() ,点
,点![]() 在线段
在线段![]() 上(不与
上(不与![]() 、
、![]() 重合),作
重合),作![]() ,
,![]() 交线段
交线段![]() 于点
于点![]() ,是否存在这样点
,是否存在这样点![]() ,使得
,使得![]() 为等腰三角形?若存在,求出
为等腰三角形?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
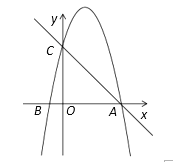
【题目】如图,抛物线![]() 与x轴交于A,B两点,与y轴交于点C,已知B(-1,0),抛物线的对称轴是直线
与x轴交于A,B两点,与y轴交于点C,已知B(-1,0),抛物线的对称轴是直线![]() .
.
(1)直接写出抛物线的解析式;
(2)点E是线段AC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,线段EF的长度最长?
(3)在抛物线是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
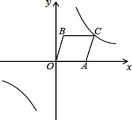
【题目】如图,A(4,0),B(1,3),以OA、OB为边作□OACB,反比例函数![]() (k≠0)的图象经过点C.则下列结论不正确的是( )
(k≠0)的图象经过点C.则下列结论不正确的是( )
A.□OACB的面积为12
B.若y<3,则x>5
C.将□OACB向上平移12个单位长度,点B落在反比例函数的图象上.
D.将□OACB绕点O旋转180°,点C的对应点落在反比例函数图象的另一分支上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明设计的“过直线外一点作已知直线的平行线”的尺规作图过程.
已知:直线![]() 及直线
及直线![]() 外一点P.
外一点P.

求作:直线![]() ,使
,使![]() .
.
作法:如图,

①在直线![]() 上取一点O,以点O为圆心,
上取一点O,以点O为圆心,![]() 长为半径画半圆,交直线
长为半径画半圆,交直线![]() 于
于![]() 两点;
两点;
②连接![]() ,以B为圆心,
,以B为圆心,![]() 长为半径画弧,交半圆于点Q;
长为半径画弧,交半圆于点Q;
③作直线![]() .
.
所以直线![]() 就是所求作的直线.
就是所求作的直线.
根据小明设计的尺规作图过程:
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明
证明:连接![]() ,
,
∵![]() ,
,
∴![]() __________.
__________.
∴![]() (______________)(填推理的依据).
(______________)(填推理的依据).
∴![]() (_____________)(填推理的依据).
(_____________)(填推理的依据).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com