
 在对口扶贫活动中,企业甲将经营状况良好的某消费品专卖店,以5.8万元的优惠价转让给了尚有5万元无息贷款还没有偿还的小型残疾人企业乙,并约定从该店经营的利润中,首先保证企业乙的全体职工每月最低生活费的开支4000元后,逐步偿还转让费(不计利息)从企业甲提供的相关资料中可知这种消费品的进价是每件12元;月销售量Q(百件)与销售单价P(元)的关系如图所示,但销售量受市场需求量的限制,维持企业的正常运转每月需最低生活费外的各种开支2000元.
在对口扶贫活动中,企业甲将经营状况良好的某消费品专卖店,以5.8万元的优惠价转让给了尚有5万元无息贷款还没有偿还的小型残疾人企业乙,并约定从该店经营的利润中,首先保证企业乙的全体职工每月最低生活费的开支4000元后,逐步偿还转让费(不计利息)从企业甲提供的相关资料中可知这种消费品的进价是每件12元;月销售量Q(百件)与销售单价P(元)的关系如图所示,但销售量受市场需求量的限制,维持企业的正常运转每月需最低生活费外的各种开支2000元.
|
|
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
|
A、-1<m<-
| ||
B、0<m<
| ||
| C、0<m<1 | ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知如图,在菱形ABCD中,CO⊥BD,垂足为点O,E为BC上一点,F为AD延长线上一点,EF交CD于点G,EG=FG=DG,连接OE、OF.
已知如图,在菱形ABCD中,CO⊥BD,垂足为点O,E为BC上一点,F为AD延长线上一点,EF交CD于点G,EG=FG=DG,连接OE、OF.| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,EC⊥CF于C,点A在CE上,点B在CF上,BD平分∠CBA,AG平分∠EAB,且直线AG交BD于D
如图,EC⊥CF于C,点A在CE上,点B在CF上,BD平分∠CBA,AG平分∠EAB,且直线AG交BD于D查看答案和解析>>
科目:初中数学 来源: 题型:
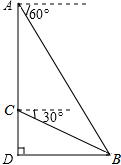 如图,哨兵在灯塔顶部A处测得遇难船只所在地B处的俯角为60°,然后下到灯塔的C处,测得B处的俯角为30°.已知AC=40米,若救援船只以5m/s 的速度从灯塔底部D处出发,几秒钟后能到达遇难船只的位置?(结果精确到个位).
如图,哨兵在灯塔顶部A处测得遇难船只所在地B处的俯角为60°,然后下到灯塔的C处,测得B处的俯角为30°.已知AC=40米,若救援船只以5m/s 的速度从灯塔底部D处出发,几秒钟后能到达遇难船只的位置?(结果精确到个位).查看答案和解析>>
科目:初中数学 来源: 题型:
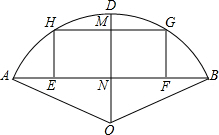 已知,如图,以O为圆心,OA为半径画弧,∠AOB=120°,弓形高ND=4厘米,矩形EFGH的两顶点E,F在弦AB上,H,G在
已知,如图,以O为圆心,OA为半径画弧,∠AOB=120°,弓形高ND=4厘米,矩形EFGH的两顶点E,F在弦AB上,H,G在 |
| AB |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在方格纸上建立平面直角坐标系,每个小正方形的边长为1.
如图,在方格纸上建立平面直角坐标系,每个小正方形的边长为1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com