
【题目】抛物线C:y=![]() x2+bx+c 交
x2+bx+c 交 ![]() 轴于点A(0,-1)且过点
轴于点A(0,-1)且过点 ![]() , P是抛物线C上一个动点,过P作PB∥OA,以P为圆心,2为半径的圆交PB于C、D两点(点D位于点C下方).
, P是抛物线C上一个动点,过P作PB∥OA,以P为圆心,2为半径的圆交PB于C、D两点(点D位于点C下方).
(1)求抛物线C的解析式;
(2)连接AP交⊙P于点E,连接DE,AC.若ΔACP是以CP为直角边的直角三角形,求∠EDC的度数;
(3)若当点P经过抛物线C上所有的点后,点D随之经过的路线被直线 ![]() 截得的线段长为8,求
截得的线段长为8,求 ![]() 的值.
的值.
【答案】
(1)解:∵A(0,-1), (4,-1)在y=![]() x2 + bx+c上,
x2 + bx+c上,
∴![]() ,
,
∴![]() ,
,
∴抛物线C的解析式为:y=![]() x2-2x-1.
x2-2x-1.
(2)解:由(1)知抛物线C的解析式为:y=![]() x2-2x-1.
x2-2x-1.
①若∠ACP=90°,即AC⊥BD,
∵A(0,-1),
则设C(x,-1),
又∵⊙P半径为2,
∴P(x,-3),D(x,-5 ),
又∵P在抛物线C上,
∴![]() x2-2x-1=-3.,
x2-2x-1=-3.,
∴x=2,
∴P(2,-3),
∴CA=CP,
∴∠APC=45°,
又∵∠APC=∠EDC+∠PED,PE=PD,
∴∠EDC=22.5°,
②若∠APC=90°,即AP⊥BD,
∵A(0,-1),PE=PD,
∴△EPD为直角三角形,
∴∠EDC=45°.
(3)解:依题可知:把 y=![]() x22x1 向下平移2个单位后得 y=
x22x1 向下平移2个单位后得 y=![]() x22x3 ,
x22x3 ,
∵对称轴为直线 x=2 ,
由已知条件得:x1=-2,x2 =6,
∴把 x=6 代入 y=![]() x22x3 ,
x22x3 ,
∴y=3,
即 a=3 .
【解析】(1)由已知条件得出一个二元一次方程组![]() ,解之 即可求出
,解之 即可求出![]() ,从而得出抛物线C的解析式为:y=
,从而得出抛物线C的解析式为:y=![]() x2-2x-1.
x2-2x-1.
(2)由(1)知抛物线C的解析式为:y=![]() x2-2x-1.分两种情况讨论:
x2-2x-1.分两种情况讨论:
① 若∠ACP=90°,即AC⊥BD,由A(0,-1),则设C(x,-1),从而得P(x,-3),D(x,-5 ),又由P在抛物线C上,得出x=2,从而得出P(2,-3),即CA=CP,根据等腰三角形的性质得出∠APC=45°,又由三角形的外角知∠APC=∠EDC+∠PED,PE=PD,从而得出∠EDC=22.5°;
②若∠APC=90°,即AP⊥BD,由A(0,-1),PE=PD,从而得出△EPD为直角三角形,即∠EDC=45°.
(3)依题可知:把 y=![]() x22x1 向下平移2个单位后得 y=
x22x1 向下平移2个单位后得 y=![]() x22x3 , 由抛物线对称轴为直线 x=2 ,从而得出x1=-2,x2 =6,把 x=6 代入 y=
x22x3 , 由抛物线对称轴为直线 x=2 ,从而得出x1=-2,x2 =6,把 x=6 代入 y=![]() x22x3 即可求出a.
x22x3 即可求出a.
【考点精析】关于本题考查的等腰直角三角形,需要了解等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°才能得出正确答案.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】如图,已知D是△ABC中的边BC上的一点,∠BAD=∠C,∠ABC的平分线交边AC于E,交AD于F,那么下列结论中错误的是( )
A.△BDF∽△BEC
B.△BFA∽△BEC
C.△BAC∽△BDA
D.△BDF∽△BAE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AB∥CD,点E,F分别在直线CD,AB上,∠BEC=2∠BEF,过点A作AG⊥BE的延长线交于点G,交CD于点N,AK平分∠BAG,交EF于点H,交BE于点M.
(1)直接写出∠AHE,∠FAH,∠KEH之间的关系:________;
(2)若∠BEF=![]() ∠BAK,求∠AHE;
∠BAK,求∠AHE;
(3)如图2,在(2)的条件下,将△KHE绕着点E以每秒5°的速度逆时针旋转,旋转时间为t,当KE边与射线ED重合时停止,则在旋转过程中,当△KHE的其中一边与△ENG的某一边平行时,直接写出此时t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现在生活人们已经离不开密码,如取款、上网等都需要密码,有一种用“因式分解”法产生的密码,方便记忆.原理是:如对于多项式![]() ,因式分解的结果是
,因式分解的结果是![]() ,若取
,若取![]() ,
,![]() 时则各个因式的值是:
时则各个因式的值是:![]() ,
,![]() ,
,![]() ,把这些值从小到大排列得到
,把这些值从小到大排列得到![]() ,于是就可以把“018162”作为一个六位数的密码.对于多项式
,于是就可以把“018162”作为一个六位数的密码.对于多项式![]() ,取
,取![]() ,
,![]() 时,请你写出用上述方法产生的密码_________.
时,请你写出用上述方法产生的密码_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的6月5日为世界环保日,为了提倡低碳环保,某公司决定购买10台节省能源的新设备,现有甲、乙两种型号的设备可供选购,经调查:购买3台甲型设备比购买2台乙型设备多花16万元,购买2台甲型设备比购买3台乙型设备少花6万元.
(1)求甲、乙两种型号设备的价格;
(2)该公司经预算决定购买节省能源的新设备的资金不超过110万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,已知甲型设备的产量为240吨/月,乙型设备的产量为180吨/月,若每月要求总产量不低于2040吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
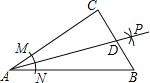
【题目】如图,在Rt△ABC中,∠C=90°,以A为圆心,以任意长为半径画弧,分别交AC、AB于点M、N,再分别以点M、N为圆心,以一个定长为半径画弧,两弧交于点P,作射线AP交BC于点D.若AC=8,BC=6,则CD的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,下列说法不正确的是( )
A.当AC=BD时,四边形ABCD是矩形
B.当AB=BC时,四边形ABCD是菱形
C.当AC⊥BD时,四边形ABCD是菱形
D.当∠DAB=90°时,四边形ABCD是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列两则材料,回答问题,材料一:定义直线y=ax+b与直线y=bx+a互为“共同体直线”,例如,直线y=x+4与直线y=4x+l互为“共同体直线”.
材料二:对于半面直角坐标系中的任意两点P1(x1,y1)、P2(x2,y2),P1、P2之两点间的直角距离d1(P1,p2)=|x1﹣x2|+|y1﹣y2|:例如:Q1(﹣3,1)、Q2(2.4)两点间的直角距离为d(Q1,Q2)=|﹣3﹣2|+|1﹣4|=8; P0(x0,y0)为一个定点,Q(x,y)是直线y=ax+b上的动点,我们把d(P0,Q)的最小值叫做Po到直线y=ax+b的直角距离.
(1)计算S(﹣2,6),T(1,3)两点间的直角距离d(S,T)= ,直线y=4x+3上的一点H(a,b)又是它的“共同体直线”上的点,求点H的坐标.
(2)对于直线y=ax+b上的任意一点M(m,n),都有点N(3m,2m﹣3n)在它的“共同体直线”上,试求点L(10,﹣![]() )到直线y=ax+b的直角距离.
)到直线y=ax+b的直角距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com