
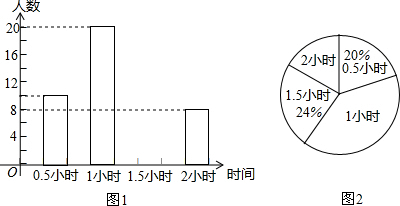
分析 (1)根据统计图找出活动时间为0.5小时的人数和百分比,计算得到答案;
(2)求出户外活动时间为1.5小时的人数,补充频数分布直方图;
(3)根据在扇形统计图中,每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°的比解答即可;
(4)求出参加户外活动的平均时间比较即可得到答案.
解答 解:(1)由直方图可知,活动时间为0.5小时的人数是10人,由扇形图可知活动时间为0.5小时的人数占20%,
则调查人数为:10÷20%=50(人);
(2)户外活动时间为1.5小时的人数:50×24%=12(人);
频数分布直方图如图: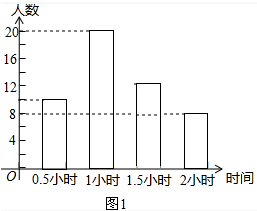
(3)表示户外活动时间2小时的扇形圆心角的度数=$\frac{8}{50}$×360°=57.6°,
(4)户外活动的平均时间=$\frac{10×0.5+20×1+12×1.5+8×2}{50}=1.18$(小时).
∵1.18>1,∴平均活动时间符合上级要求;
全市参加户外活动时间符合要求的学生为:$\frac{20+12+8}{50}×50000=40000$(人).
点评 本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年广东省梅州市七年级下学期第一次月考数学试卷(解析版) 题型:填空题
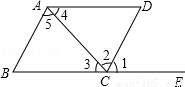
如图,现给出下列条件:①∠1=∠B,②∠2=∠5,③∠3=∠4,④∠1=∠D,⑤∠B+∠BCD=180°,其中能够得到AB∥CD的条件是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
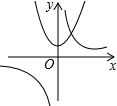 如图,抛物线y=x2+1与双曲线y=$\frac{k}{x}$的交点A的横坐标是1,则关于x的不等式$\frac{k}{x}-{x}^{2}$-1>0的解集是( )
如图,抛物线y=x2+1与双曲线y=$\frac{k}{x}$的交点A的横坐标是1,则关于x的不等式$\frac{k}{x}-{x}^{2}$-1>0的解集是( )| A. | x>1 | B. | x<-1 | C. | 0<x<1 | D. | -1<x<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com