
【题目】如图,在![]() 中,
中,![]() ,
,![]() .点
.点![]() 是线段
是线段![]() 上的一点,连结
上的一点,连结![]() ,过点
,过点![]() 作
作![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,与过点
,与过点![]() 且垂直于
且垂直于![]() 的直线相交于点
的直线相交于点![]() ,连结
,连结![]() .给出以下四个结论:①
.给出以下四个结论:①![]() ;②若点
;②若点![]() 是
是![]() 的中点,则
的中点,则![]() ;③当
;③当![]() 、
、![]() 、
、![]() 、
、![]() 四点在同一个圆上时,
四点在同一个圆上时,![]() ;④若
;④若![]() ,则
,则![]() .其中正确的结论序号是( )
.其中正确的结论序号是( )

A. ①②B. ①②③C. ③④D. ①②③④
【答案】B
【解析】
(1)由△AFG∽△BFC,可确定结论①正确;
(2)先证明△ABG≌△BCD(ASA),得到AG=BD,再通过点![]() 是
是![]() 的中点,利用(1)中得到的
的中点,利用(1)中得到的![]() ,得到
,得到![]() ,在Rt△ABC中,可得AC=
,在Rt△ABC中,可得AC=![]() AB,即可得到AF=
AB,即可得到AF=![]() AB,故结论②正确;
AB,故结论②正确;
(3)当B、C、F、D四点在同一个圆上时,由圆内接四边形的性质得到∠2=∠ACB由于∠ABC=90°,AB=BC,得到∠ACB=∠CAB=45°,于是得到∠CFD=∠AFD=90°,根据垂径定理得到DF=DB,故③正确;
(4)因为![]() =
=![]() ,所以AF=
,所以AF=![]() AC ,
AC ,![]() ,所以S△ABF=
,所以S△ABF=![]() S△ABC,又S△BDF=
S△ABC,又S△BDF=![]() S△ABF,所以S△ABC=12S△BDF,由此确定结论④错误.
S△ABF,所以S△ABC=12S△BDF,由此确定结论④错误.

解:
(1)∵![]() ,
,![]()
∴BC∥AG,
∴∠G=∠FBC
∠GAF=∠FCB
∴△AFG∽△BFC,
∴![]() ,
,
又AB=BC,
∴![]() .
.
故结论①正确;
(2)如图,∵∠1+∠3=90°,∠1+∠4=90°,
∴∠3=∠4.
在△ABG与△BCD中 ,
,
∴△ABG≌△BCD(ASA),
∴AG=BD,
∵点![]() 是
是![]() 的中点,
的中点,![]()
∴AG=BD=![]() AB=
AB=![]() BC
BC
∴![]()
∴![]()
∵在Rt△ABC中,AB=BC
∴AC=![]() AB
AB
∴AF=![]() AB
AB
故结论②正确;
(3)当B、C、F、D四点在同一个圆上时,
∴∠2=∠ACB,
∵∠ABC=90°,AB=BC,
∴∠ACB=∠CAB=45°,
∴∠2=45°,
∴∠CFD=∠AFD=90°,
∴CD是B、C、F、D四点所在圆的直径,
∵BG⊥CD,
∴DF与BD对应的弧相等,
∴DF=DB,故③正确;
(4)∵![]() ,AG=BD,
,AG=BD,![]() ,
,
∴![]() ,
,
∴![]()
∴AF=![]() AC,
AC,
∴S△ABF=![]() S△ABC,
S△ABC,
∴S△BDF=![]() S△ABF,
S△ABF,
∴S△BDF=![]() S△ABC,即S△ABC=12S△BDF.
S△ABC,即S△ABC=12S△BDF.
故结论④错误;
正确的是①②③,故选:B.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
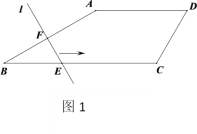
【题目】如图1,在四边形![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,直线
,直线![]() .当直线
.当直线![]() 沿射线
沿射线![]() 方向,从点
方向,从点![]() 开始向右平移时,直线
开始向右平移时,直线![]() 与四边形
与四边形![]() 的边分别相交于点
的边分别相交于点![]() 、
、![]() .设直线
.设直线![]() 向右平移的距离为
向右平移的距离为![]() ,线段
,线段![]() 的长为
的长为![]() ,且
,且![]() 与
与![]() 的函数关系如图2所示,则四边形
的函数关系如图2所示,则四边形![]() 的周长是_____.
的周长是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 经过点(2,3),对称轴为直线x =1.
经过点(2,3),对称轴为直线x =1.
(1)求抛物线的表达式;
(2)如果垂直于y轴的直线l与抛物线交于两点A(![]() ,
, ![]() ),B(
),B(![]() ,
, ![]() ),其中
),其中![]() ,
, ![]() ,与y轴交于点C,求BC
,与y轴交于点C,求BC![]() AC的值;
AC的值;
(3)将抛物线向上或向下平移,使新抛物线的顶点落在x轴上,原抛物线上一点P平移后对应点为点Q,如果OP=OQ,直接写出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个儿童游乐场所,由于周末小朋友较多,老板计划将场地扩建,扩建前平面图为△ABC,BC=10米,∠ABC=∠ACB=36°,扩建后顶点D在BA的延长线上,且∠BDC=90°,求扩建后AB边增加部分AD的长.(结果精确到0.1米.参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.32,sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】企业举行“爱心一日捐”活动,捐款金额分为五个档次,分别是50元,100元,150元,200元,300元.宣传小组随机抽取部分捐款职工并统计了他们的捐款金额,绘制成两个不完整的统计图,请结合图表中的信息解答下列问题:
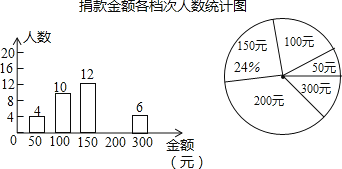
(1)宣传小组抽取的捐款人数为 人,请补全条形统计图;
(2)统计的捐款金额的中位数是 元;
(3)在扇形统计图中,求100元所对应扇形的圆心角的度数;
(4)已知该企业共有500人参与本次捐款,请你估计捐款总额大约为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边由长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AB是O的直径,点C在O上,且点C为弧BE的中点,连接AE并延长交BC延长线于点D.

(1)判断△ABD的形状,并说明理由;
(2)过点C作CM⊥AD,垂足为点F,如图2.求证:CF是O的切线;
(3)若O的半径为3,DF=1,求sinB的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
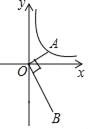
【题目】如图,已知点A是反比例函数y=![]() (x>0)的图象上的一个动点,连接OA,OB⊥OA,且OB=2OA,那么经过点B的反比例函数图象的表达式为( )
(x>0)的图象上的一个动点,连接OA,OB⊥OA,且OB=2OA,那么经过点B的反比例函数图象的表达式为( )
A. y=﹣![]() B. y=
B. y=![]() C. y=﹣
C. y=﹣![]() D. y=
D. y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】传统节日“端午节”的早晨,小文妈妈为小文准备了四个粽子作早点:一个枣馅粽,一个肉馅粽,两个花生馅粽,四个粽子除内部馅料不同外,其它一切均相同.
(1)小文吃前两个粽子刚好都是花生馅粽的概率为 ;
(2)若妈妈在早点中给小文再增加一个花生馅的粽子,则小文吃前两个粽子都是花生馅粽的可能性是否会增大?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com