
【题目】已知抛物线![]() 的图象经过点A(2,-8),求:
的图象经过点A(2,-8),求:
(1)该抛物线的解析式;
(2)判断点B(3,-18)是否在该抛物线上;
(3)求出此抛物线上纵坐标是-50的点的坐标.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
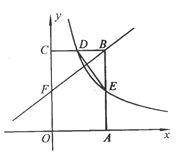
【题目】如图,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(2,4),双曲线![]() 的图像经过BC的中点D,且与AB交于点E,连接DE.
的图像经过BC的中点D,且与AB交于点E,连接DE.
(1)求k的值及点E的坐标;
(2)若点F是边上一点,且△FBC∽△DEB,求直线FB的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形 ![]() 中,点
中,点![]() 是射线
是射线 ![]() 上一个动点.连接
上一个动点.连接![]() ,
,![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,连接
的中点,连接![]() 交
交![]() 于点
于点![]() .
.
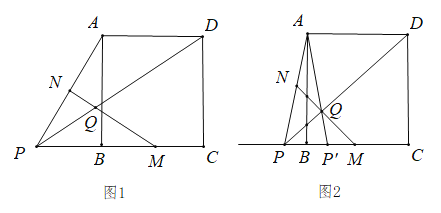
(1)如图 1,当点![]() 在线段
在线段 ![]() 的延长线上时,请判断
的延长线上时,请判断![]() 的形状,并说明理由.
的形状,并说明理由.
(2)如图 2,正方形 的边长为 4,点![]() 与点
与点![]() 关于直线
关于直线 ![]() 对称,且点
对称,且点![]() 在线段
在线段 ![]() 上.连接
上.连接![]() ,若点
,若点 ![]() 恰好在直线
恰好在直线![]() 上,求
上,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
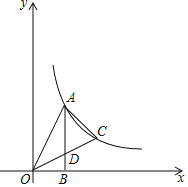
【题目】如图,在平面直角坐标系中,点O为坐标原点,直角三角形AOB的直角顶点B在x轴正半轴上,点A在第一象限,OB=2,tan∠AOB=2.
(1)求图象经过点A的反比例函数的解析式;
(2)点C是(1)中反比例函数图象上一点,连接OC交AB于点D,连接AC,若D为OC中点,求△ADC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(1)如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .
(2)如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.
(3)从概率的角度分析,你建议小明在第几题使用“求助”.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.
的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.
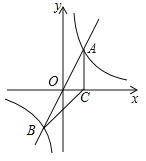
(1)求k的值;
(2)x轴上是否存在一点D,使△ABD为直角三角形?若存在,求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
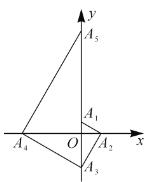
【题目】如图,已致点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴的正半轴上,且
轴的正半轴上,且![]() .过点
.过点![]() 作
作![]() ,交
,交![]() 轴于点
轴于点![]() ;过点
;过点![]() 作
作![]() ,交
,交![]() 轴于点
轴于点![]() ;过点
;过点![]() 作
作![]() ,交
,交![]() 轴于点
轴于点![]() ;……;按此规律进行下去,则点
;……;按此规律进行下去,则点![]() 的坐标为( )
的坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
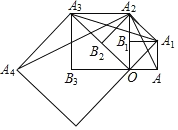
【题目】如图,四边形 OAA1B1 是边长为 1 的正方形,以对角线 OA1 为边作第二个正方形 OA1A2B2,连接 AA2,得到△ AA1A2;再以对角线 OA2 为边作第三个正方形 OA2A3B3,连接 A1A3,得到△A1A2A3;再以对角线 OA3 为边作第 四个正方形,连接 A2A4,得到△A2A3A4……记△AA1A2、△A1A2A3、△A2A3A4 的面积分别为 S1、S2、S3,如此下 去,则 S2019=_____ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com