
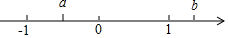 化简求值:
化简求值:分析 (1)由于3<$\sqrt{13}$<4,由此可得$\sqrt{13}$的整数a的值;由于$\sqrt{b}$=3,根据算术平方根的定义可求b,再代入$\sqrt{ab+54}$计算,进一步求得平方根.
(2)利用数轴得出各项符号,进而利用二次根式和绝对值的性质化简求出即可.
解答 解:(1)∵3<$\sqrt{13}$<4,
∴a=3,
∵$\sqrt{b}$=3,
∴b=9,
∴$\sqrt{ab+54}$=$\sqrt{3×9+54}$=9,
∴$\sqrt{ab+54}$的平方根是±3;
(2)由数轴可得:-1<a<0<1<b,
则a+1<0,b-1>0,a-b<0,
则$\sqrt{(a+1)^{2}}$+2$\sqrt{(b-1)^{2}}$-|a-b|
=-a-1+2(b-1)+(a-b)
=-a-1+2b-2+a-b
=b-3.
点评 本题考查了算术平方根与平方根的定义和估算无理数的大小,熟记概念,先判断所给的无理数的近似值是解题的关键.


科目:初中数学 来源: 题型:解答题
 如图,沿长方形ABCD的对角线AC对折,点B落在点E上,AE与CD交于F点,
如图,沿长方形ABCD的对角线AC对折,点B落在点E上,AE与CD交于F点,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
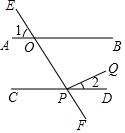 如图,直线AB、CD被直线EF所截,交点为O、P,PQ⊥EF,垂足为P,如果∠1=60°,∠2=30°,那么直线AB、CD平行吗?为什么?
如图,直线AB、CD被直线EF所截,交点为O、P,PQ⊥EF,垂足为P,如果∠1=60°,∠2=30°,那么直线AB、CD平行吗?为什么?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com