
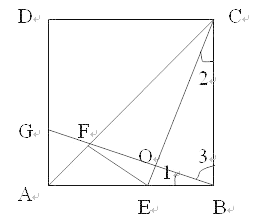
【题目】如图,在正方ABCD中,E是AB边上任一点,BG⊥CE,垂足为O,交AC于点F,交AD于点G.
(1)证明:BE=AG;
(2)E位于什么位置时,∠AEF=∠CEB?说明理由.

【答案】(1)见解析;(2)当点E位于线段AB中点时,∠AEF=∠CEB ,理由见解析
【解析】
(1) 根据正方形的性质利用ASA判定△GAB≌△EBC,根据全等三角形的对应边相等可得到AG=BE;
(2) 利用SAS判定△GAF≌△EAF,从而得到∠AGF=∠AEF,由△GAB≌△EBC可得到∠AGF=∠CEB,则∠AEF=∠CEB.
(1)证明:∵四边形ABCD是正方形
∴∠ABC=∠BAD=90°,∴∠1+∠3=90°,
∵BG⊥CE,∴∠BOC=90°∴∠2+∠3=90°,
∴∠1=∠2,
在△GAB和△EBC中,
∵∠GAB=∠EBC=90°,AB=BC,∠1=∠2,
∴△GAB≌△EBC (ASA) ,
∴AG=BE;
(2)解:当点E位于线段AB中点时,∠AEF=∠CEB ,
理由如下:若当点E位于线段AB中点时,则AE=BE,
由(1)可知,AG=BE,
∴AG=AE,
∵四边形ABCD是正方形,
∴∠GAF=∠EAF=45°,
又∵AF=AF,
∴△GAF≌△EAF (SAS),
∴∠AGF=∠AEF,
由(1)知,△GAB≌△EBC,
∴∠AGF=∠CEB,
∴∠AEF=∠CEB.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中边AB的垂直平分线分别交BC,AB于点D,E,AE=3cm,△ADC的周长为9cm,则△ABC的周长是( )

A. 10cm B. 12cm C. 15cm D. 17cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | ||
高中部 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在期末考试来临之际,同学们都进入紧张的复习阶段,为了了解同学们晚上的睡眠情况,现对年级部分同学进行了调查统计,并制成如下两幅不完整的统计图:(其中A代表睡眠时间8小时左右,B代表睡眠时间6小时左右,C代表睡眠时间4小时左右,D代表睡眠时间5小时左右,E代表睡眠时间7小时左右),其中扇形统计图中“E”的圆心角为90°,请你结合统计图所给信息解答下列问题:
(1)共抽取了 名同学进行调查,同学们的睡眠时间的中位数是 小时左右,并将条形统计图补充完整;
(2)请你估计年级每个学生的平均睡眠时间约多少小时?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面说法中错误的有( )
①如果△ABC的三个内角满足∠A=∠C﹣∠B,那么△ABC一定是直角三角形;
②如果一个三角形只有一条高在三角形的内部,那么这个三角形一定是钝角三角形;
③若m>n,则ma2>na2;
④方程3x+2y=9的非负整数解是x=1,y=3;
⑤由三条线段首尾顺次连接所组成的图形叫做三角形.
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家禽养殖场,用总长为110m的围栏靠墙(墙长为22m)围成如图所示的三块矩形区域,矩形AEHG与矩形CDEF面积都等于矩形BFHG面积的一半,设AD长为xm,矩形区域ABCD的面积为ym2 . 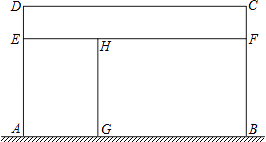
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)当x为何值时,y有最大值?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以![]() 的边
的边![]() 、
、![]() 为边的等边三角
为边的等边三角![]() 和等边三角形
和等边三角形![]() ,四边形
,四边形![]() 是平行四边形.
是平行四边形.
![]() 当
当![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是矩形;
是矩形;
![]() 当
当![]() 满足什么条件时,平行四边形
满足什么条件时,平行四边形![]() 不存在;
不存在;
![]() 当
当![]() 分别满足什么条件时,平行四边形
分别满足什么条件时,平行四边形![]() 是菱形,正方形?
是菱形,正方形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分别是BG,AC的中点.
(1)求证:DE=DF,DE⊥DF;
(2)连接EF,若AC=10,求EF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com