
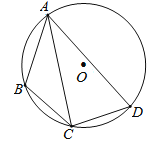
【题目】如图,在⊙O的内接四边形ABCD中,AB=3,AD=5,∠BAD=60°,点C为弧BD的中点,则AC的长是 .
【答案】![]() .
.
【解析】
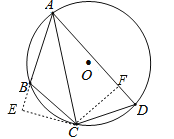
试题分析:过C作CE⊥AB于E,CF⊥AD于F,则∠E=∠CFD=∠CFA=90°,∵点C为弧BD的中点,∴![]() ,∴∠BAC=∠DAC,BC=CD,∵CE⊥AB,CF⊥AD,∴CE=CF,∵A、B、C、D四点共圆,∴∠D=∠CBE,在△CBE和△CDF中,∵∠CBE=∠D,∠E=∠CFD,CE=CF,∴△CBE≌△CDF,∴BE=DF,在△AEC和△AFC中,∵∠E=∠AFC,∠EAC=∠FAC,AC=AC,∴△AEC≌△AFC,∴AE=AF,设BE=DF=x,∵AB=3,AD=5,∴AE=AF=x+3,∴5=x+3+x,解得:x=1,即AE=4,∴AC=
,∴∠BAC=∠DAC,BC=CD,∵CE⊥AB,CF⊥AD,∴CE=CF,∵A、B、C、D四点共圆,∴∠D=∠CBE,在△CBE和△CDF中,∵∠CBE=∠D,∠E=∠CFD,CE=CF,∴△CBE≌△CDF,∴BE=DF,在△AEC和△AFC中,∵∠E=∠AFC,∠EAC=∠FAC,AC=AC,∴△AEC≌△AFC,∴AE=AF,设BE=DF=x,∵AB=3,AD=5,∴AE=AF=x+3,∴5=x+3+x,解得:x=1,即AE=4,∴AC=![]() =
=![]() ,故答案为:
,故答案为:![]() .
.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
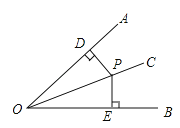
【题目】证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程,下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.
已知:如图,∠AOC=∠BOC,点P在OC上,求证: .
请你补全已知和求证,并写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】质地均匀的骰子六个面分别刻有1到6的点数,掷两次骰子,得到向上一面的两个点数,则下列事件中,发生可能性最大的是( )
A.点数都是偶数
B.点数的和为奇数
C.点数的和小于13
D.点数的和小于2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学初一(二)班5位教师决定带领本班a名学生在五一期间在元旦期间去珠海长隆海洋王国旅游,每张票的价格为350元,A旅行社的收费标准为:教师全价,学生半价;而B旅行社的收费标准为:不分教师、学生,一律六折优惠.
(1)分别用代数式表示参加这两家旅行社所需的费用;
A旅行社所需费用为 元,B旅行社所需费用为 元,
(2)如果这5位教师要带领该班30名学生参加旅游,你认为选择哪一家旅行社较为合算,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列证明:
如图,已知DE⊥AC于点E,BC⊥AC于点C,FG⊥AB于点G,∠1=∠2,求证:CD⊥AB.
证明:∵DE⊥AC,BC⊥AC(已知),
∴DE∥(),
∴∠2=(两直线平行,内错角相等),
∵∠1=∠2,(已知),
∴∠1=(),
∴GF∥CD(),
∵FG⊥AB(已知),
∴CD⊥AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
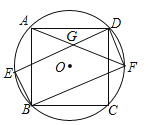
【题目】正方形ABCD内接于⊙O,如图所示,在劣弧![]() 上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,求证:
上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,求证:
(1)四边形EBFD是矩形;
(2)DG=BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
【发现】
如图∠ACB=∠ADB=90°,那么点D在经过A,B,C三点的圆上(如图①)
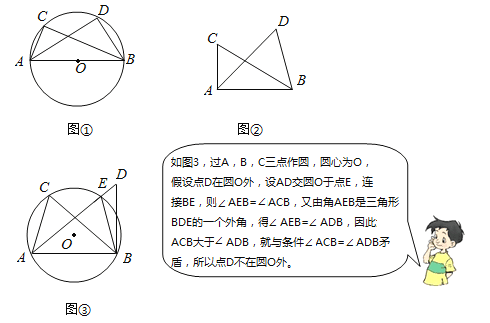
【思考】
如图②,如果∠ACB=∠ADB=a(a≠90°)(点C,D在AB的同侧),那么点D还在经过A,B,C三点的圆上吗?
请证明点D也不在⊙O内.
【应用】
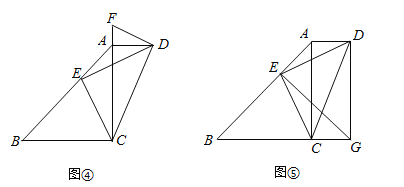
利用【发现】和【思考】中的结论解决问题:若四边形ABCD中,AD∥BC,∠CAD=90°,点E在边AB上,CE⊥DE.
(1)作∠ADF=∠AED,交CA的延长线于点F(如图④),求证:DF为Rt△ACD的外接圆的切线;
(2)如图⑤,点G在BC的延长线上,∠BGE=∠BAC,已知sin∠AED=![]() ,AD=1,求DG的长.
,AD=1,求DG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com