
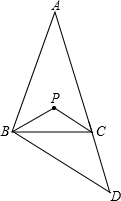
 如图,在△ABC中,AB=AC,∠A=40°,延长AC到D,使CD=BC,点P是△ABD的内心,则∠BPC=145°.
如图,在△ABC中,AB=AC,∠A=40°,延长AC到D,使CD=BC,点P是△ABD的内心,则∠BPC=145°. 分析 由P为△ABD的内心,得出P点必在∠BAC的角平分线上,由于AB=AC,根据等腰三角形的性质可知:P点必在BC的垂直平分线上,即BP=PC,△BPC也是等腰三角形,欲求∠BPC,必先求出∠PBC的度数.等腰△ABC中,已知了顶角∠A的度数,可求得∠ABC、∠ACB的度数;由于CB=CD,∠ACB是△ABC的外角,由此可求出∠D和∠CBD的度数;由于P是△ABD的内心,则PB平分∠ABD,由此可求得∠PBD的度数,根据∠PBC=∠PBD-∠CBD可求出∠PBC的度数,由此得解.
解答 解:△ABC中,AB=AC,∠A=40°;
∴∠ABC=∠ACB=70°;
∵P是△ABD的内心,
∴P点必在等腰△ABC底边BC的垂直平分线上,
∴PB=PC,∠BPC=180°-2∠PBC;
在△CBD中,CB=CD,
∴∠CBD=∠D=$\frac{1}{2}$∠ACB=35°;
∵P是△ABD的内心,
∴PB平分∠ABD,
∴∠PBD=$\frac{1}{2}$∠ABD=$\frac{1}{2}$(∠ABC+∠CBD)=52.5°,
∴∠PBC=∠PBD-∠CBD=52.5°-35°=17.5°;
∴∠BPC=180°-2∠PBC=145°.
故答案为:145°.
点评 本题考查了三角形的内切圆与内心、等腰三角形的性质、线段垂直平分线的性质、三角形内角和定理等知识;此题比较复杂,综合性强,熟记三角形的内心性质是解决问题的关键.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
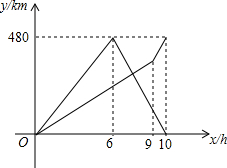 在一条笔直的公路,有A、B两地,甲从A地到B地,同时乙从B地到A地,途中两人相遇,乙到达A地后,立即按原路返回,遇到甲后两人一起回到B地.如图分别是两人各自离出发地的距离y(千米)与出发的时间x(小时)之间的函数图象,根据图象信息解答下列问题:
在一条笔直的公路,有A、B两地,甲从A地到B地,同时乙从B地到A地,途中两人相遇,乙到达A地后,立即按原路返回,遇到甲后两人一起回到B地.如图分别是两人各自离出发地的距离y(千米)与出发的时间x(小时)之间的函数图象,根据图象信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com