
【题目】已知,直线![]() ,点
,点![]() 为平面内一点,连接
为平面内一点,连接![]() 与
与![]() .
.

(1)如图1,点![]() 在直线
在直线![]() 、
、![]() 之间,若
之间,若![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
(2)如图2,点![]() 在直线
在直线![]() 、
、![]() 之间,
之间,![]() 与
与![]() 的角平分线相交于点
的角平分线相交于点![]() ,写出
,写出![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
(3)如图3,点![]() 在直线
在直线![]() 下方,
下方,![]() 与
与![]() 的角平分线相交于点
的角平分线相交于点![]() ,直接写出
,直接写出![]() 与
与![]() 的数量关系.
的数量关系.
【答案】(1)∠APC=80°;(2)∠AKC=![]() ∠APC;(3)∠AKC=
∠APC;(3)∠AKC=![]() ∠APC.
∠APC.
【解析】
(1)先过P作PE∥AB,根据平行线的性质即可得到∠APE=∠BAP,∠CPE=∠DCP,再根据∠APC=∠APE+∠CPE=∠BAP+∠DCP进行计算即可;
(2)过K作KE∥AB,根据KE∥AB∥CD,可得∠AKE=∠BAK,∠CKE=∠DCK,进而得到∠AKC=∠AKE+∠CKE=∠BAK+∠DCK,同理可得,∠APC=∠BAP+∠DCP,再根据角平分线的定义,得出∠BAK+∠DCK=![]() ∠BAP+
∠BAP+![]() ∠DCP=
∠DCP=![]() (∠BAP+∠DCP)=
(∠BAP+∠DCP)=![]() ∠APC,进而得到∠AKC=
∠APC,进而得到∠AKC=![]() ∠APC;
∠APC;
(3)过K作KE∥AB,根据KE∥AB∥CD,可得∠BAK=∠AKE,∠DCK=∠CKE,进而得到∠AKC=∠AKE-∠CKE=∠BAK-∠DCK,同理可得,∠APC=∠BAP-∠DCP,再根据角平分线的定义,得出∠BAK-∠DCK=![]() ∠BAP-
∠BAP-![]() ∠DCP=
∠DCP=![]() (∠BAP-∠DCP)=
(∠BAP-∠DCP)=![]() ∠APC,进而得到∠AKC=
∠APC,进而得到∠AKC=![]() ∠APC.
∠APC.
(1)如图1,过P作PE∥AB,
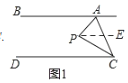
∵AB∥CD,
∴PE∥AB∥CD,
∴∠APE=∠BAP,∠CPE=∠DCP,
∴∠APC=∠APE+∠CPE=∠BAP+∠DCP=60°+20°=80°;
(2)∠AKC=![]() ∠APC.
∠APC.
理由:如图2,过K作KE∥AB,

∵AB∥CD,
∴KE∥AB∥CD,
∴∠AKE=∠BAK,∠CKE=∠DCK,
∴∠AKC=∠AKE+∠CKE=∠BAK+∠DCK,
过P作PF∥AB,
同理可得,∠APC=∠BAP+∠DCP,
∵∠BAP与∠DCP的角平分线相交于点K,
∴∠BAK+∠DCK=![]() ∠BAP+
∠BAP+![]() ∠DCP=
∠DCP=![]() (∠BAP+∠DCP)=
(∠BAP+∠DCP)= ![]() ∠APC,
∠APC,
∴∠AKC=![]() ∠APC;
∠APC;
(3)∠AKC=![]() ∠APC.
∠APC.
理由:如图3,过K作KE∥AB,

∵AB∥CD,
∴KE∥AB∥CD,
∴∠BAK=∠AKE,∠DCK=∠CKE,
∴∠AKC=∠AKE∠CKE=∠BAK∠DCK,
过P作PF∥AB,
同理可得,∠APC=∠BAP∠DCP,
∵∠BAP与∠DCP的角平分线相交于点K,
∴∠BAK∠DCK=![]() ∠BAP
∠BAP![]() ∠DCP=
∠DCP=![]() (∠BAP∠DCP)=
(∠BAP∠DCP)=![]() ∠APC,
∠APC,
∴∠AKC=![]() ∠APC.
∠APC.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】某商店在2014年至2016年期间销售一种礼盒.2014年,该商店用3500元购进了这种礼盒并且全部售完;2016年,这种礼盒的进价比2014年下降了11元/盒,该商店用2400元购进了与2014年相同数量的礼盒也全部售完,礼盒的售价均为60元/盒.
(1)2014年这种礼盒的进价是多少元/盒?
(2)若该商店每年销售这种礼盒所获利润的年增长率相同,问年增长率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC直角三角形,延长AB到D,使BD=BC,在BC上取BE=AB,连接DE.△ABC顺时针旋转后能与△EBD重合,那么:
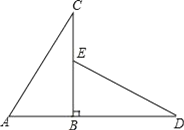
(1)旋转中心是哪一点?旋转角是多少度?
(2)AC与DE的关系怎样?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个有进水管与出水管的容器,从某时刻开始的4分内只进水不出水,在随后的若干分内既进水又出水,之后只有出水不进水,每分钟的进水量和出水量是两个常数,容器内的水量![]() (单位:升)与时间
(单位:升)与时间![]() (单位:分)之间的关系如图所示,则进水速度是______升/分,出水速度是______升/分,
(单位:分)之间的关系如图所示,则进水速度是______升/分,出水速度是______升/分,![]() 的值为______.
的值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数 y=-2x+5 的图像分别与 x 轴,y 轴交于点A、B,以线段AB 为边在第一象限内作等腰 RtABC,BAC=90 ,求过 B、C 两点的直线的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象上部分点的横坐标x与纵坐标y的对应值如下表:

那么关于它的图象,下列判断正确的是( )
A. 开口向上 B. 与x轴的另一个交点是(3,0)
C. 与y轴交于负半轴 D. 在直线x=1的左侧部分是下降的
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)求值:![]()
(2)用消元法解方程组 时,两位同学的解法如下:
时,两位同学的解法如下:
解法一:
由①-②,得![]() .
.
解法二:
由②得,![]() ,③
,③
把①代入③,得![]() .
.
①反思:上述两个解题过程中有无计算错误?若有误,请在错误处打“×”.
②请选择一种你喜欢的方法,完成解答.
(3)求不等式组 的正整数解.
的正整数解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市中学生举行足球联赛,共赛了17轮(即每队均需参赛17场),记分办法是胜-场得3分。平场得1分,负一场得0分.
(1)在这次足球赛中,若小虎足球队踢平场数与踢负场数相同,共积16分,求该队胜了几场;
(2)在这次足球赛中,若小虎足球队总积分仍为16分,且踢平场数是踢负场数的整数倍,试推算小虎足球队踢负场数的情况有几种,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com