
【题目】对于抛物线y=x2﹣2mx+m2+m﹣2,当﹣1≤x≤2时,函数的最小值为m,则m的值为( )
A.![]() 或
或![]() B.
B.![]() 或
或![]()
C.![]() 或
或![]() D.
D.![]() 或
或![]()
【答案】A
【解析】
根据抛物线y=x2﹣2mx+m2+m﹣2,当﹣1≤x≤2时,函数的最小值为m,可以得到该抛物线的对称轴,然后利用分类讨论的方法可以得到m的值,本题得以解决.
解:∵抛物线y=x2﹣2mx+m2+m﹣2=(x﹣m)2+m﹣2,
∴该抛物线的对称轴是直线x=m,
∵当﹣1≤x≤2时,函数的最小值为m,
∴当m≤﹣1时,在﹣1≤x≤2时,y随x增大而增大,所以当x=﹣1时,y为最小值m,即(﹣1﹣m)2+m﹣2=m,得m=﹣1﹣![]() ;
;
当﹣1<m<2时,当x=m时,取得最小值,即m﹣2=m,此方程无解;
当m≥2时,在﹣1≤x≤2时,y随x增大而减小,所以当x=2时,y为最小值m,即(2﹣m)2+m﹣2=m,得m=2+![]() ;
;
由上可得,m的值是﹣1﹣![]() 或2+
或2+![]() ,
,
故选:A.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,将二次函数y=![]() (x-2)2+1的图像沿y轴向上平移得到一条新的二次函数图像,其中A(1,m),B(4,n)平移后对应点分别是A′、B′,若曲线AB所扫过的面积为12(图中阴影部分),则新的二次函数对应的函数表达是__________________.
(x-2)2+1的图像沿y轴向上平移得到一条新的二次函数图像,其中A(1,m),B(4,n)平移后对应点分别是A′、B′,若曲线AB所扫过的面积为12(图中阴影部分),则新的二次函数对应的函数表达是__________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
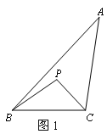
【题目】在直角坐标系中,已知抛物线![]() (a<0)与x轴交于A、B两点(点A在点B左侧),与y轴负半轴交于点C,顶点为D,已知
(a<0)与x轴交于A、B两点(点A在点B左侧),与y轴负半轴交于点C,顶点为D,已知![]() :S四边形ACBD=1:4.
:S四边形ACBD=1:4.
(1)求点D的坐标(用仅含c的代数式表示);
(2)若tan∠ACB=![]() ,求抛物线的解析式.
,求抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
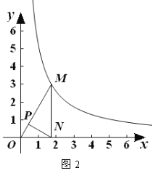
【题目】定义:点P是△ABC内部或边上的点(顶点除外),在△PAB,△PBC,△PCA中,若至少有一个三角形与△ABC相似,则称点P是△ABC的自相似点.
例如:如图1,点P在△ABC的内部,∠PBC=∠A,∠PCB=∠ABC,则△BCP∽△ABC,故点P为△ABC的自相似点.
请你运用所学知识,结合上述材料,解决下列问题:
在平面直角坐标系中,点M是曲线C:![]()
![]() 上的任意一点,点N是x轴正半轴上的任意一点.
上的任意一点,点N是x轴正半轴上的任意一点.
(1) 如图2,点P是OM上一点,∠ONP=∠M, 试说明点P是△MON的自相似点; 当点M的坐标是![]() ,点N的坐标是
,点N的坐标是![]() 时,求点P 的坐标;
时,求点P 的坐标;
(2) 如图3,当点M的坐标是![]() ,点N的坐标是
,点N的坐标是![]() 时,求△MON的自相似点的坐标;
时,求△MON的自相似点的坐标;
(3) 是否存在点M和点N,使△MON无自相似点,?若存在,请直接写出这两点的坐标;若不存在,请说明理由.
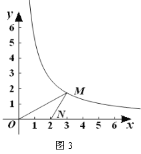
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=-x+3与x轴,y轴分别交于B,C两点,抛物线y=-x2+bx+c经过B,C两点,点A是抛物线与x轴的另一个交点.
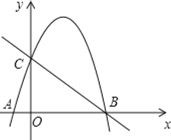
(1)求此抛物线的函数解析式;
(2)在抛物线上是否存在点P,使S△PAB=2S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织学生书法比赛,对参赛作品按A、B、C、D四个等级进行了评定.现随机取部分学生书法作品的评定结果进行分析,并绘制扇形统计图和条形统计图如下:

根据上述信息完成下列问题:
(1)求这次抽取的样本的容量;
(2)请在图②中把条形统计图补充完整;
(3)已知该校这次活动共收到参赛作品750份,请你估计参赛作品达到B级以上(即A级和B级)有多少份?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.

(1)求证:BG=DE;
(2)若E为AD中点,FH=2,求菱形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以M,N为圆心,以大于![]() MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为________.
MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】舍利生生塔位于晋祠南瑞,建于隋开皇年间,宋代重修,清乾隆十六年(1751年)重建.七屋八角,琉璃瓦顶,远远望去,高耸的古塔,映衬着蓝天白云,甚是壮观.原塔内每层均有佛像,开4门8窗,凭窗远眺,晋祠内外美景可一览无余.如果在夕阳西下时欣赏宝塔,还会出现——天云锦、满塔光辉的壮丽景观,被誉为“宝塔披霞”.某数学“综合与实践”小组的同学把“测量舍利生生塔高”作为一项课题活动,他们制定了测量方案,并利用课余时间完成了实地测量,测量结果如表:
课题 | 测量舍利生生塔高 | |||
测量示意图 |
| 说明:某同学在地面上选择点C,使用手持测角仪,测得此时楼顶A的仰角∠AHE=α,沿CB方向前进到点D,测量出C,D之间的距离CD=xm,在点D使用手持测角仪,测得此时楼顶A的仰角∠AFE=β | ||
测量数据 | α的度数 | β的度数 | CD的长度 | 该同学眼睛离地面的距离HC |
24° | 37° | 32m | 1.76m | |
… | … | |||
(1)请帮助该小组的同学根据上表中的测量数据,求塔高AB.(结果精确到1m;参考数据:sin24°≈0.41,cos24°≈0.91,tan24°≈0.45,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
(2)该小组要写出一份完整的课题活动报告,除上表中的项目外,你认为还需要补充哪些项目?(写出一个即可)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com