
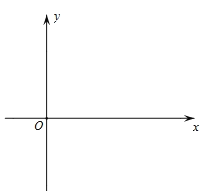
【题目】在直角坐标系中,已知抛物线![]() (a<0)与x轴交于A、B两点(点A在点B左侧),与y轴负半轴交于点C,顶点为D,已知
(a<0)与x轴交于A、B两点(点A在点B左侧),与y轴负半轴交于点C,顶点为D,已知![]() :S四边形ACBD=1:4.
:S四边形ACBD=1:4.
(1)求点D的坐标(用仅含c的代数式表示);
(2)若tan∠ACB=![]() ,求抛物线的解析式.
,求抛物线的解析式.
【答案】(1)D(2,![]() );(2)抛物线的解析式为:
);(2)抛物线的解析式为:![]() ,或
,或![]() ,或
,或![]() .
.
【解析】
(1)直接代入顶点坐标公式化简即可;
(2)先由![]() :S四边形ACBD=1:4,得到等底三角形的面积之比
:S四边形ACBD=1:4,得到等底三角形的面积之比![]() :
:![]() =1:3,而求出
=1:3,而求出![]() ,解析式化为
,解析式化为![]() ,求得A(1,0),B(3,0),过点B作
,求得A(1,0),B(3,0),过点B作![]() 的延长线于点H,得到
的延长线于点H,得到![]() ∽
∽![]() ,依据相似的性质、锐角三角函数,用c表示AH、BH,最后在三角形ABH中依据勾股定理求出c,即可得到解析式.
,依据相似的性质、锐角三角函数,用c表示AH、BH,最后在三角形ABH中依据勾股定理求出c,即可得到解析式.
解:(1)抛物线![]() 的顶点D的坐标为
的顶点D的坐标为![]()
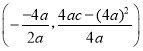 ,
,
∴顶点D的坐标为(2,![]() );
);
(2)∵![]() 与y轴负半轴交于点C,
与y轴负半轴交于点C,
∴C(0,c),![]() ,
,
过点D作![]() 轴于点G,则
轴于点G,则![]()
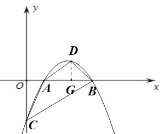
∵![]() :S四边形ACBD=1:4,
:S四边形ACBD=1:4,
∴![]() :
:![]() =1:3,
=1:3,
则![]() ,即
,即![]() ,
,
∴![]() ,
,
∴抛物线的解析式为:![]() 或
或![]() ,
,![]() =
=![]() ,
,![]() ,
,
∴令![]() =0,解得
=0,解得![]()
∴A(1,0),B(3,0),![]() ,
,
过点B作![]() 的延长线于点H,
的延长线于点H,

∴![]() (对顶角相等),
(对顶角相等),
∴![]() ∽
∽![]() ,tan∠ACB=
,tan∠ACB=![]() =
=![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
![]() ,
,
∴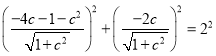 ,
,
∴![]() =0,(
=0,(![]() )
)
∴![]() -1或-3或-2+
-1或-3或-2+![]() (舍)或-2-
(舍)或-2-![]() ,
,
∴抛物线的解析式为:![]() ,或
,或![]() ,或
,或![]() .
.


 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:
【题目】抛物线![]() (
(![]() 为常数)与
为常数)与![]() 轴交于点
轴交于点![]() 和
和![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 为抛物线顶点.
为抛物线顶点.
(Ⅰ)当![]() 时,求点
时,求点![]() ,点
,点![]() 的坐标;
的坐标;
(Ⅱ)①若顶点![]() 在直线
在直线![]() 上时,用含有
上时,用含有![]() 的代数式表示
的代数式表示![]() ;
;
②在①的前提下,当点![]() 的位置最高时,求抛物线的解析式;
的位置最高时,求抛物线的解析式;
(Ⅲ)若![]() ,当
,当![]() 满足
满足![]() 值最小时,求
值最小时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形![]() 中,
中,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,连接
的中点,连接![]() 、
、![]() ,
,![]() 和
和![]() 交于点
交于点![]() .
.
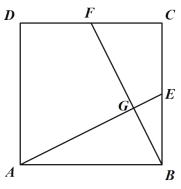
(1)如图1,求证:![]() ;
;
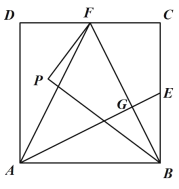
(2)如图2,作![]() 关于
关于![]() 对称的图形
对称的图形![]() ,连接
,连接![]() ,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于正方形
,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于正方形![]() 面积的
面积的![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△AEF中,∠EAF=45°,AG⊥EF于点G,现将△AEG沿AE折叠得到△AEB,将△AFG沿AF折叠得到△AFD,延长BE和DF相交于点C.
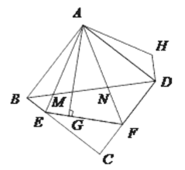
(1)试判断四边形ABCD的形状,并给出证明;
(2)连接BD分别交AE、AF于点M、N,将△ABM绕点A逆时针旋转,使AB与AD重合,得到△ADH,试判断线段MN、ND、DH之间的数量关系,并说明理由.
(3)若EG=2,GF=3,BM=2,求AG、MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象交x轴于A、B两点,交y轴于点D,点B的坐标为
的图象交x轴于A、B两点,交y轴于点D,点B的坐标为![]() ,顶点C的坐标为
,顶点C的坐标为![]() .
.
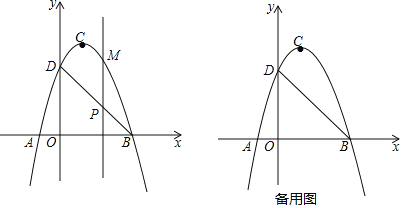
![]() 求二次函数的解析式和直线BD的解析式;
求二次函数的解析式和直线BD的解析式;
![]() 点P是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M,当点P在第一象限时,求线段PM长度的最大值;
点P是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M,当点P在第一象限时,求线段PM长度的最大值;
![]() 在抛物线上是否存在异于B、D的点Q,使
在抛物线上是否存在异于B、D的点Q,使![]() 中BD边上的高为
中BD边上的高为![]() ?若存在求出点Q的坐标;若不存在请说明理由.
?若存在求出点Q的坐标;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中(如图),已知抛物线
中(如图),已知抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,,抛物线的顶点为点
,,抛物线的顶点为点![]() ,对称轴与
,对称轴与![]() 轴交于点
轴交于点![]() .
.

(1)求抛物线的表达式及点![]() 的坐标;
的坐标;
(2)点![]() 是
是![]() 轴正半轴上的一点,如果
轴正半轴上的一点,如果![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,点![]() 是位于
是位于![]() 轴左侧抛物线上的一点,如果
轴左侧抛物线上的一点,如果![]() 是以
是以![]() 为直角边的直角三角形,求点
为直角边的直角三角形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,对角线AC、BD交于O点,DE∥AC,CE∥BD.
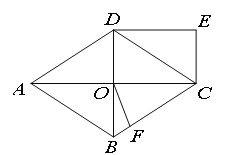
(1)求证:四边形OCED为矩形;
(2)在BC上截取CF=CO,连接OF,若AC=16,BD=12,求四边形OFCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知矩形![]() 的顶点
的顶点![]() ,动点
,动点![]() ,
,![]() 同时从
同时从![]() 点出发,点
点出发,点![]() 沿射线
沿射线![]() 方向以每秒
方向以每秒![]() 个单位的速度运动,点
个单位的速度运动,点![]() 沿线段
沿线段![]() 方向以每秒
方向以每秒![]() 个单位的速度运动,当点
个单位的速度运动,当点![]() 到达点
到达点![]() 时,点
时,点![]() ,
,![]() 同时停止运动,连接
同时停止运动,连接![]() ,设运动时间为
,设运动时间为![]() (秒).
(秒).
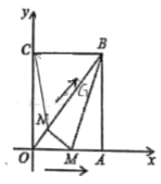
(1)求证![]() ;
;
(2)当点![]() 运动到点
运动到点![]() 时,若双曲线
时,若双曲线![]() 的图象恰好过点
的图象恰好过点![]() ,试求
,试求![]() 的值;
的值;
(3)连接![]() ,当
,当![]() 为何值时,
为何值时,![]() 为等腰三角形.
为等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com