
【题目】在平面直角坐标系![]() 中(如图),已知抛物线
中(如图),已知抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,,抛物线的顶点为点
,,抛物线的顶点为点![]() ,对称轴与
,对称轴与![]() 轴交于点
轴交于点![]() .
.

(1)求抛物线的表达式及点![]() 的坐标;
的坐标;
(2)点![]() 是
是![]() 轴正半轴上的一点,如果
轴正半轴上的一点,如果![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,点![]() 是位于
是位于![]() 轴左侧抛物线上的一点,如果
轴左侧抛物线上的一点,如果![]() 是以
是以![]() 为直角边的直角三角形,求点
为直角边的直角三角形,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或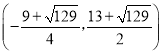
【解析】
(1)将点A、B 代入抛物线![]() ,即可求出抛物线解析式,再化为顶点式即可;
,即可求出抛物线解析式,再化为顶点式即可;
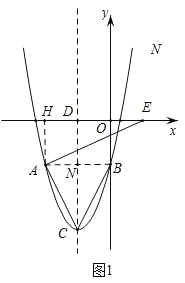
(2)如图1,连接AB,交对称轴于点N,则N(-![]() ,-2),利用相等角的正切值相等即可求出EH的长,OE的长,可写出点E的坐标;
,-2),利用相等角的正切值相等即可求出EH的长,OE的长,可写出点E的坐标;
(3)分∠EAP=90°和∠AEP=90°两种情况讨论,通过相似的性质,用含t的代数式表示出点P的坐标,可分别求出点P的坐标.
解:(1)(1)将点A(-3,-2)、B (0,-2)代入抛物线![]() ,
,
得,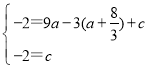 ,
,
解得,a=![]() ,c=-2,
,c=-2,
∴y=![]() x2+4x-2
x2+4x-2
=![]() (x+
(x+![]() )2-5,
)2-5,
∴抛物线解析式为y=![]() x2+4x-2,顶点C的坐标为(-
x2+4x-2,顶点C的坐标为(-![]() ,-5);
,-5);
(2)如图1,连接AB,交对称轴于点N,则N(-![]() ,-2),
,-2),
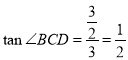 ,则
,则![]() ,
,
过![]() 作
作![]() ,
,![]() ,
,
则![]() ,
,
∵OH=3,
∴OE=1,
∴![]()
(3)①如图2,当∠EAP=90°时,
∵∠HEA+∠HAE=90,∠HAE+∠MAP=90°,
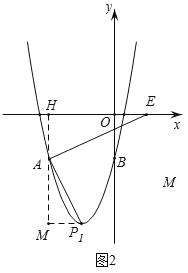
∴∠HEA=∠MAP,
又∠AHE=∠PMA=90°,
![]() ,
,
则![]() ,设
,设![]() ,则
,则![]()
将![]() 代入
代入![]()
得![]() (舍),
(舍),![]() ,
,
∴![]()
②如图3,当∠AEP=90°时,
∵∠EAG+∠AEG=90°,∠AEG+∠PEN=90°,
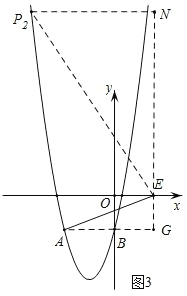
∴∠AEG=∠EPN,
又∵∠N=∠G=90°,
∴![]() ,则
,则![]()
设![]() ,则
,则![]()
将![]() 代入
代入![]()
得![]() ,
,![]() (舍),
(舍),
∴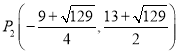
综上所述:![]() ,
,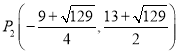


科目:初中数学 来源: 题型:
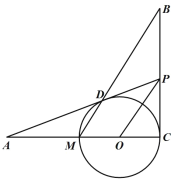
【题目】如图,已知BCAC,圆心O在AC上,点M与点C分别是AC与⊙O的交点,点D是MB与⊙O的交点,点P是AD延长线与BC的交点,且ADAOAMAP,连接OP.
(1)证明:MD//OP;
(2)求证:PD是⊙O的切线;
(3)若AD24,AMMC,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两个不透明的布袋,甲袋中有两个完全相同的小球,分别标有数字﹣1和3;乙袋中有三个完全相同的小球,分别标有数字1、0和﹣3.小丽先从甲袋中随机取出一个小球,记录下小球上的数字为x;再从乙袋中随机取出一个小球,记录下小球上的数字为y,设点A的坐标为(x,y).
(1)请用表格或树状图列出点A所有可能的坐标;
(2)求点A在反比例函数y=![]() 图象上的概率.
图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
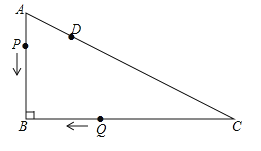
【题目】如图,Rt△ABC中,∠B=90°,AB=3cm,BC=4cm.点D在AC上,AD=1cm,点P从点A出发,沿AB匀速运动;点Q从点C出发,沿C→B→A→C的路径匀速运动.两点同时出发,在B点处首次相遇后,点P的运动速度每秒提高了2cm,并沿B→C→A的路径匀速运动;点Q保持速度不变,并继续沿原路径匀速运动,两点在D点处再次相遇后停止运动,设点P原来的速度为xcm/s.
(1)点Q的速度为 cm/s(用含x的代数式表示).
(2)求点P原来的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,已知抛物线![]() (a<0)与x轴交于A、B两点(点A在点B左侧),与y轴负半轴交于点C,顶点为D,已知
(a<0)与x轴交于A、B两点(点A在点B左侧),与y轴负半轴交于点C,顶点为D,已知![]() :S四边形ACBD=1:4.
:S四边形ACBD=1:4.
(1)求点D的坐标(用仅含c的代数式表示);
(2)若tan∠ACB=![]() ,求抛物线的解析式.
,求抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料,并按要求完成相应的任务:
莱昂哈德·欧拉(Leonhard Euler)是瑞士数学家,在数学上经常见到以他的名字命名的重要常数、公式和定理,下面是欧拉发现的一个定理:在△ABC 中,R 和 r 分别为外接圆和内切圆的半径,O 和 I 分别为其外心和内心,则OI ![]() R
R![]() 2Rr .
2Rr .
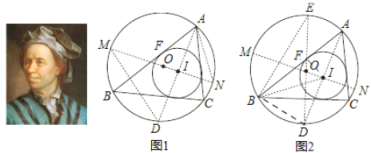
下面是该定理的证明过程(借助了第(2)问的结论):
延长AI 交⊙O 于点 D,过点 I 作⊙O 的直径 MN,连接 DM,AN.
∵∠D=∠N,∴∠DMI=∠NAI(同弧所对的圆周角相等),
∴△MDI∽△ANI.∴![]() ,∴ IA ID IM IN ①
,∴ IA ID IM IN ①
如图②,在图 1(隐去 MD,AN)的基础上作⊙O 的直径DE,连接BE,BD,BI,IF
∵DE 是⊙O 的直径,∴∠DBE=90°.
∵⊙I 与 AB 相切于点 F,∴∠AFI=90°,
∴∠DBE=∠IFA.
∵∠BAD=∠E(同弧所对圆周角相等),
∴△AIF∽△EDB.
∴![]() ,∴
,∴![]() ②,
②,
由(2)知:![]() ,
,
∴![]()
又∵![]() ,
,
∴ 2Rr(R d )(R d ) ,
∴ R![]() d
d![]() 2Rr
2Rr
∴ d ![]() R
R![]() 2Rr
2Rr
任务:(1)观察发现: IM R d , IN (用含R,d 的代数式表示);
(2)请判断 BD 和 ID 的数量关系,并说明理由.(请利用图 1 证明)
(3)应用:若△ABC 的外接圆的半径为 6cm,内切圆的半径为 2cm,则△ABC 的外心与内心之间的距离为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
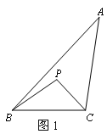
【题目】定义:点P是△ABC内部或边上的点(顶点除外),在△PAB,△PBC,△PCA中,若至少有一个三角形与△ABC相似,则称点P是△ABC的自相似点.
例如:如图1,点P在△ABC的内部,∠PBC=∠A,∠PCB=∠ABC,则△BCP∽△ABC,故点P为△ABC的自相似点.
请你运用所学知识,结合上述材料,解决下列问题:
在平面直角坐标系中,点M是曲线C:![]()
![]() 上的任意一点,点N是x轴正半轴上的任意一点.
上的任意一点,点N是x轴正半轴上的任意一点.
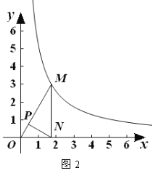
(1) 如图2,点P是OM上一点,∠ONP=∠M, 试说明点P是△MON的自相似点; 当点M的坐标是![]() ,点N的坐标是
,点N的坐标是![]() 时,求点P 的坐标;
时,求点P 的坐标;
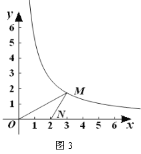
(2) 如图3,当点M的坐标是![]() ,点N的坐标是
,点N的坐标是![]() 时,求△MON的自相似点的坐标;
时,求△MON的自相似点的坐标;
(3) 是否存在点M和点N,使△MON无自相似点,?若存在,请直接写出这两点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织学生书法比赛,对参赛作品按A、B、C、D四个等级进行了评定.现随机取部分学生书法作品的评定结果进行分析,并绘制扇形统计图和条形统计图如下:

根据上述信息完成下列问题:
(1)求这次抽取的样本的容量;
(2)请在图②中把条形统计图补充完整;
(3)已知该校这次活动共收到参赛作品750份,请你估计参赛作品达到B级以上(即A级和B级)有多少份?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.
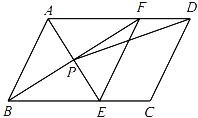
(1)求证:四边形ABEF是菱形;
(2)若AB=4,AD=6,∠ABC=60°,求tan∠ADP的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com