
【题目】如图,在ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.
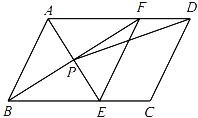
(1)求证:四边形ABEF是菱形;
(2)若AB=4,AD=6,∠ABC=60°,求tan∠ADP的值.
【答案】(1)见解析;(2)![]()
【解析】
(1)先证明四边形是平行四边形,再根据平行四边形和角平分线的性质可得AB=BE,AB=AF,AF=BE,从而证明四边形ABEF是菱形;
(2)作PH⊥AD于H,根据四边形ABEF是菱形,∠ABC=60°,AB=4,得到AB=AF=4,∠ABF=∠ADB=30°,AP⊥BF,从而得到PH=3,DH=5,然后利用锐角三角函数的定义求解即可.
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠DAE=∠AEB.
∵AE是角平分线,
∴∠DAE=∠BAE.
∴∠BAE=∠AEB.
∴AB=BE.
同理AB=AF.
∴AF=BE.
∴四边形ABEF是平行四边形.
∵AB=BE,
∴四边形ABEF是菱形.
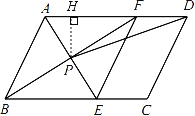
(2)解:作PH⊥AD于H,
∵四边形ABEF是菱形,∠ABC=60°,AB=4,
∴AB=AF=4,∠ABF=∠AFB=30°,AP⊥BF,
∴AP=![]() AB=2,
AB=2,
∴PH=![]() ,AH=1,
,AH=1,
∴DH=5,
∴tan∠ADP=![]() =
=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中(如图),已知抛物线
中(如图),已知抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,,抛物线的顶点为点
,,抛物线的顶点为点![]() ,对称轴与
,对称轴与![]() 轴交于点
轴交于点![]() .
.

(1)求抛物线的表达式及点![]() 的坐标;
的坐标;
(2)点![]() 是
是![]() 轴正半轴上的一点,如果
轴正半轴上的一点,如果![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,点![]() 是位于
是位于![]() 轴左侧抛物线上的一点,如果
轴左侧抛物线上的一点,如果![]() 是以
是以![]() 为直角边的直角三角形,求点
为直角边的直角三角形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
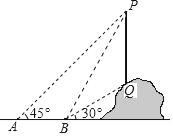
【题目】如图,从点A看一山坡上的电线杆PQ,观测点P的仰角是45°,向前走6m到达B点,测得顶端点P和杆底端点Q的仰角分别是60°和30°,则该电线杆PQ的高度( )
A. 6+2![]() B. 6+
B. 6+![]() C. 10﹣
C. 10﹣![]() D. 8+
D. 8+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知矩形![]() 的顶点
的顶点![]() ,动点
,动点![]() ,
,![]() 同时从
同时从![]() 点出发,点
点出发,点![]() 沿射线
沿射线![]() 方向以每秒
方向以每秒![]() 个单位的速度运动,点
个单位的速度运动,点![]() 沿线段
沿线段![]() 方向以每秒
方向以每秒![]() 个单位的速度运动,当点
个单位的速度运动,当点![]() 到达点
到达点![]() 时,点
时,点![]() ,
,![]() 同时停止运动,连接
同时停止运动,连接![]() ,设运动时间为
,设运动时间为![]() (秒).
(秒).
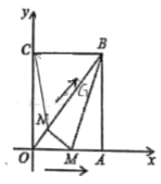
(1)求证![]() ;
;
(2)当点![]() 运动到点
运动到点![]() 时,若双曲线
时,若双曲线![]() 的图象恰好过点
的图象恰好过点![]() ,试求
,试求![]() 的值;
的值;
(3)连接![]() ,当
,当![]() 为何值时,
为何值时,![]() 为等腰三角形.
为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
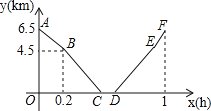
【题目】从甲地到乙地,先是一段上坡路,然后是一段平路,小明骑车从甲地出发,到达乙地后休息一段时间,然后原路返回甲地.假设小明骑车在上坡、平路、下坡时分别保持匀速前进,已知小明骑车上坡的速度比平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km,设小明出发xh后,到达离乙地ykm的地方,图中的折线ABCDEF表示y与x之间的函数关系.
(1)小明骑车在平路上的速度为 km/h,他在乙地休息了 h.
(2)分别求线段AB、EF所对应的函数关系式.
(3)从甲地到乙地经过丙地,如果小明两次经过丙地的时间间隔为0.85h,求丙地与甲地之间的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ACB中,∠C=90°,AC=3,BC=4,O是BC的中点,到点O的距离等于![]() BC的所有点组成的图形记为G,图形G与AB交于点D.
BC的所有点组成的图形记为G,图形G与AB交于点D.

(1)补全图形并求线段AD的长;
(2)点E是线段AC上的一点,当点E在什么位置时,直线ED与 图形G有且只有一个交点?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
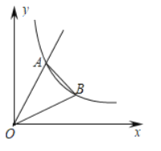
【题目】如图,正比例函数y1=k1x的图象与反比例函数y2=![]() (x>0)的图象相交于点A(
(x>0)的图象相交于点A(![]() ,2
,2![]() ),点B是反比例函数图象上一点,它的横坐标是3,连接OB,AB,则△AOB的面积是_____.
),点B是反比例函数图象上一点,它的横坐标是3,连接OB,AB,则△AOB的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阿里巴巴电商对贫困地区一种特色农产品进行网上销售,按原价每件300元出售,一个月可卖出100件,通过市场调查发现,售价每件降低10元,月销售件数增加20件
(1)已知该农产品的成本是每件200元,在保持月利润不变的情况下,尽快下手完毕,则售价应定为多少元?
(2)小红返校在附近线下超市也有该农产品销售,并且标价为每件300元,买五送一,在(1)的条件下,小红想要用最优惠的价格购买38件该农产品,应该选择在线上购买还是线下超市购买?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com