
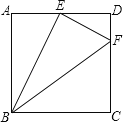
【题目】在正方形ABCD中,点E为AD中点,DF=![]() CD,则下列说法:(1)BE⊥EF;(2)图中有3对相似三角形;(3)E到BF的距离为
CD,则下列说法:(1)BE⊥EF;(2)图中有3对相似三角形;(3)E到BF的距离为![]() AB;(4)
AB;(4)![]() =
=![]() .其中正确的有( )
.其中正确的有( )
A.4个 B.3个 C.2个 D.1个
【答案】B
【解析】
试题分析:根据正方形的性质得到AD=AB=BC=CD,∠A=∠ABC=C=∠D=90°,由于点E为AD中点,DF=![]() CD,于是得到
CD,于是得到![]() =2,推出△ABE∽△DEF,根据相似三角形的性质得到∠ABE=∠DEF,根据平角的定义得到∠BEF=90°,于是求得BE⊥EF;故①正确;根据相似三角形的性质得到
=2,推出△ABE∽△DEF,根据相似三角形的性质得到∠ABE=∠DEF,根据平角的定义得到∠BEF=90°,于是求得BE⊥EF;故①正确;根据相似三角形的性质得到![]() ,等量代换得到
,等量代换得到![]() ,推出△ABE∽△BEF,于是得到△ABE∽△BEF∽△DEF,即可得到图中有3对相似三角形;故②正确;根据相似三角形的性质得到∠ABE=∠EBF,根据角平分线的性质得到E到BF的距离=AE,于是得到E到BF的距离为
,推出△ABE∽△BEF,于是得到△ABE∽△BEF∽△DEF,即可得到图中有3对相似三角形;故②正确;根据相似三角形的性质得到∠ABE=∠EBF,根据角平分线的性质得到E到BF的距离=AE,于是得到E到BF的距离为![]() AB;故③正确;设DF=1,则AE=DE=2,AB=BC=CD=4,由勾股定理得到BE=
AB;故③正确;设DF=1,则AE=DE=2,AB=BC=CD=4,由勾股定理得到BE=![]() =2
=2![]() ,EF=
,EF=![]() =
=![]() ,求得S△BEF=
,求得S△BEF=![]() BEEF=5,S△BCF=
BEEF=5,S△BCF=![]() BCCF=
BCCF=![]() =6于是得到
=6于是得到![]() =
=![]() ,故④错误.
,故④错误.
解:在正方形ABCD中,
∵AD=AB=BC=CD,∠A=∠ABC=C=∠D=90°,
∵点E为AD中点,DF=![]() CD,
CD,
∴![]() =2,
=2,
∴△ABE∽△DEF,
∴∠ABE=∠DEF,
∵∠AEB+∠ABE=90°,
∴∠AEB+∠DEF=90°,
∴∠BEF=90°,
∴BE⊥EF;故①正确;
∵△ABE∽△DEF,
∴![]() ,
,
∴![]() ,
,
∵∠A=∠BEF=90°,
∴△ABE∽△BEF,
∴△ABE∽△BEF∽△DEF,
∴图中有3对相似三角形;故②正确;
∵△ABE∽△BEF,
∴∠ABE=∠EBF,
∴E到BF的距离=AE,
∴E到BF的距离为![]()
设DF=1,则AE=DE=2,AB=BC=CD=4,
∴CF=3,
∴BE=![]() =2
=2![]() ,EF=
,EF=![]() =
=![]() ,
,
∴S△BEF=![]() BEEF=5,S△BCF=
BEEF=5,S△BCF=![]() BCCF=
BCCF=![]() =6
=6
∴![]() =
=![]() ,故④错误,
,故④错误,
故选B.



科目:初中数学 来源: 题型:
【题目】一个饲养场,鸡的只数与兔的只数之和是70,鸡、兔的腿数之和为196,若设鸡的只数是x,依题意可列方程为
A. 2x=196+4(70-x) B. 4x+2(70-x)=196
C. 2x+4(70-x)=196 D. 2x+196=4(70-x)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一列不全为零的数除了第一个数和最后一个数外,每个数都等于前后与它相邻的两数之和,则称这列数具有“波动性质”.已知一列数共有2016个,且具有“波动性质”,则这2016个数的和为( )
A.﹣64 B.0 C.18 D.64
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋中,红色、黑色、白色的玻璃球共有60个,除颜色外,形状、大小、质地等完全相同。小刚通过多次摸球实验后发现其中摸到红色、黑色球的频率稳定在15%和45%,则口袋中白色球的个数很可能是( )
A. 9个 B. 24个 C. 27个 D. 30个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解方程x2-4x+1=0时,配方后所得的方程是( )
A. (x-2)2=1 B. (x-2)2=-1 C. (x-2)2=3 D. (x+2)2=3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O为△ABC的外接圆,直线l与⊙O相切与点P,且l∥BC.
(1)请仅用无刻度的直尺,在⊙O中画出一条弦,使这条弦将△ABC分成面积相等的两部分(保留作图痕迹,不写作法);
(2)请写出证明△ABC被所作弦分成的两部分面积相等的思路.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com