
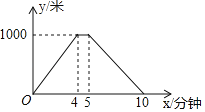
【题目】在一段长为1000的笔直道路AB上,甲、乙两名运动员均从A点出发进行往返跑训练.已知乙比甲先出发30秒钟,甲距A点的距离y(米)与其出发的时间x(分钟)的函数图象如图所示,乙的速度是150米分钟,且当乙到达B点后立即按原速返回.
(1)当x为何值时,两人第一次相遇?
(2)当两人第二次相遇时,求甲的总路程.
【答案】(1)当x为0.75分钟时,两人第一次相遇;(2)当两人第二次相遇时,甲行驶的总路程是1109.375米.
【解析】
(1)根据函数图象中的数据可以计算出当x为何值时,两人第一次相遇;
(2)根据函数图象中的数据可以计算出当两人第二次相遇时,甲行驶的总路程.
(1)甲的速度为:100÷4=250米/分钟,
令250x=150(x![]() ),
),
解得,x=0.75,
答:当x为0.75分钟时,两人第一次相遇;
(2)当x=5时,
乙行驶的路程为:150×(5![]() )=825<1000,
)=825<1000,
∴甲乙第二次相遇的时间为:5![]() 5
5![]() (分钟),
(分钟),
则当两人第二次相遇时,甲行驶的总路程为:1000+(5![]() 5)×250=1109.375(米),
5)×250=1109.375(米),
答:当两人第二次相遇时,甲行驶的总路程是1109.375米.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:
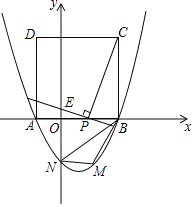
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,以
,以![]() 为边在
为边在![]() 轴上方作正方形
轴上方作正方形![]() ,点
,点![]() 是
是![]() 轴上一动点,连接
轴上一动点,连接![]() ,过点
,过点![]() 作
作![]() 的垂线与
的垂线与![]() 轴交于点
轴交于点![]() .
.
(1)求该抛物线的函数关系表达式;
(2)当点![]() 在线段
在线段![]() (点
(点![]() 不与
不与![]() 重合)上运动至何处时,线段
重合)上运动至何处时,线段![]() 的长有最大值?并求出这个最大值;
的长有最大值?并求出这个最大值;
(3)在第四象限的抛物线上任取一点![]() ,连接
,连接![]() .请问:
.请问:![]() 的面积是否存在最大值?若存在,求出此时点
的面积是否存在最大值?若存在,求出此时点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】天门山索道是世界最长的高山客运索道,位于张家界天门山景区.在一次检修维护中,检修人员从索道A处开始,沿A﹣B﹣C路线对索道进行检修维护.如图:已知![]() 米,
米,![]() 米,AB与水平线
米,AB与水平线![]() 的夹角是
的夹角是![]() ,BC与水平线
,BC与水平线![]() 的夹角是
的夹角是![]() .求:本次检修中,检修人员上升的垂直高度
.求:本次检修中,检修人员上升的垂直高度![]() 是多少米?(结果精确到1米,参考数据:
是多少米?(结果精确到1米,参考数据:![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:某列车平均提速80km/h,用相同的时间,该列车提速前行驶300km,提速后比提速前多行驶200km,求该列车提速前的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有如图所示的甲、乙、丙、丁四个生产基地.现决定在其中一个基地修建总仓库,以方便公司对各基地生产的产品进行集中存储.已知甲、乙、丙、丁各基地的产量之比等于4:5:4:2,各基地之间的距离之比a:b:c:d:e=2:3:4:3:3(因条件限制,只有图示中的五条运输渠道),当产品的运输数量和运输路程均相等时,所需的运费相等.若要使总运费最低,则修建总仓库的最佳位置为( )
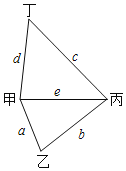
A. 甲B. 乙C. 丙D. 丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校近几年来通过“书香校园”主题系列活动,倡导学生整本阅读纸质课外书籍.下面的统计图是该校2013年至2018年纸质书人均阅读量的情况,根据统计图提供的信息,下列推断不合理的是( )

A. 从2013年到2016年,该校纸质书人均阅读量逐年增长
B. 2013年至2018年,该校纸质书人均阅读量的中位数是![]() 本
本
C. 2013年至2018年,该校纸质书人均阅读量的极差是![]() 本
本
D. 2013年至2018年,该校后三年纸质书人均阅读量总和是前三年纸质书人均阅读量总和的![]() 倍
倍
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学数学兴趣小组在一次课外学习与探究中遇到一些新的数学符号,他们将其中某些材料摘录如下:
对于三个实,数![]() ,
,![]() ,
,![]() ,用
,用![]() 表示这三个数的平均数,用
表示这三个数的平均数,用![]() 表示这三个数中最小的数,例如
表示这三个数中最小的数,例如![]()
![]() =4,
=4,![]() ,
,![]() .请结合上述材料,解决下列问题:
.请结合上述材料,解决下列问题:
(1)①![]() _____,
_____,
②![]() _____;
_____;
(2)若![]() ,则
,则![]() 的取值范围为_____;
的取值范围为_____;
(3)若![]() ,求
,求![]() 的值;
的值;
(4)如果![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘轮船在相距90千米的甲、乙两地之间匀速航行,从甲地到乙地顺流航行用6小时,逆流航行比顺流航行多用4小时.
(1)求该轮船在静水中的速度和水流速度;
(2)若在甲、乙两地之间建立丙码头,使该轮船从甲地到丙地和从乙地到丙地所用的航行时间相同,问甲、丙两地相距多少干米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠ACB=90°,∠CAB=a,且sina=![]() ,I为内心,则△ABC的内切圆半径r与△BIC的外接圆半径R之比为( )
,I为内心,则△ABC的内切圆半径r与△BIC的外接圆半径R之比为( )
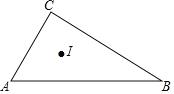
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com