
【题目】如图,在△ABC中,AB=AC,以为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.
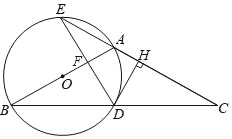
(1)求证:DH是圆O的切线;
(2)若![]() =
=![]() ,求证A为EH的中点;
,求证A为EH的中点;
(3)若EA=EF=2,求圆O的半径.
【答案】(1)见解析;(2)见解析;(3)⊙O的半径为1+![]()
【解析】
(1)根据同圆的半径相等和等边对等角证明∠ODB=∠OBD=∠ACB,则DH⊥AC,则DH是圆O的切线;
(2)先证明∠E=∠B=∠C,得△EDC是等腰三角形,证明△AEF∽△ODF,则![]() ,设OD=3x,AE=2x,可知EC=8x,根据等腰三角形三线合一得EH=CH=4x,从而得结论;
,设OD=3x,AE=2x,可知EC=8x,根据等腰三角形三线合一得EH=CH=4x,从而得结论;
(3)设⊙O的半径为r,即OD=OB=r,证明DF=OD=r,则DE=DF+EF=r+2,BD=CD=DE=r+2,证明△BFD∽△EFA,列比例式为![]() ,列方程即可求出r的值.
,列方程即可求出r的值.
(1)证明:连接OD,如图,
∵OB=OD,
∴△ODB是等腰三角形,
∠OBD=∠ODB①,
在△ABC中,∵AB=AC,
∴∠ABC=∠ACB②,
由①②得:∠ODB=∠OBD=∠ACB,
∴OD∥AC,
∵DH⊥AC,
∴DH⊥OD,
∴DH是圆O的切线;
(2)解:如图,在⊙O中,∵∠E=∠B,
∴由(1)可知:∠E=∠B=∠C,
∴△EDC是等腰三角形,
∵![]()
∵AE∥OD,
∴△AEF∽△ODF,
∴![]()
设OD=3x,AE=2x,
∵AO=BO,OD∥AC,
∴BD=CD,
∴AC=2OD=6x,
∴EC=AE+AC=2x+6x=8x,
∵ED=DC,DH⊥EC,
∴EH=CH=4x,
∴AH=EH﹣AE=4x﹣2x=2x,
∴AE=AH,
∴A是EH的中点;
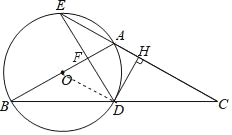
(3)解:如图,设⊙O的半径为r,即OD=OB=r,
∵EF=EA,
∴∠EFA=∠EAF,
∵OD∥EC,
∴∠FOD=∠EAF,
则∠FOD=∠EAF=∠EFA=∠OFD,
∴DF=OD=r,
∴DE=DF+EF=r+2,
∴BD=CD=DE=r+2,
在⊙O中,∵∠BDE=∠EAB,
∴∠BFD=∠EFA=∠EAB=∠BDE,
∴BF=BD,△BDF是等腰三角形,
∴BF=BD=r+2,
∴AF=AB﹣BF=2OB﹣BF=2r﹣(2+r)=r﹣2,
∵∠BFD=∠EFA,∠B=∠E,
∴△BFD∽△EFA,
∴![]()
∴![]()
解得:r1=1+![]() ,r2=1﹣
,r2=1﹣![]() (舍),
(舍),
经检验地,r=1+![]() 时,
时,![]() ,故根成立
,故根成立
综上所述,⊙O的半径为1+![]() .
.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】某市政府规定:若本市企业按生产成本价提供产品给大学生销售,则政府给该企业补偿![]() 补偿额
补偿额![]() 批发价
批发价![]() 生产成本价
生产成本价![]() 销售量
销售量![]() 大学生小明投资销售本市企业生产的一种新型节能灯,调查发现,每月销售量
大学生小明投资销售本市企业生产的一种新型节能灯,调查发现,每月销售量![]() 件
件![]() 与销售单价
与销售单价![]() 元
元![]() 之间的关系近似满足一次函数:
之间的关系近似满足一次函数:![]() 已知这种节能灯批发价为每件12元,设它的生产成本价为每件m元
已知这种节能灯批发价为每件12元,设它的生产成本价为每件m元![]()
(1)当![]() 时.
时.
①若第一个月的销售单价定为20元,则第一个月政府要给该企业补偿多少元?
②设所获得的利润为![]() 元
元![]() ,当销售单价定为多少元时,每月可获得最大利润?
,当销售单价定为多少元时,每月可获得最大利润?
(2)物价部门规定,这种节能灯的销售单价不得超过30元![]() 今年三月小明获得赢利,此时政府给该企业补偿了920元,若m,x都是正整数,求m的值.
今年三月小明获得赢利,此时政府给该企业补偿了920元,若m,x都是正整数,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (m是常数)
(m是常数)
(1)证明:不论m取何值时,该二次函数图象总与x轴有两个交点;
(2)若![]() 、
、![]() 是该二次函数图象上的两个不同点,求二次函数解析式和m的值;
是该二次函数图象上的两个不同点,求二次函数解析式和m的值;
(3)若![]() ,
,![]() 在函数图象上,且
在函数图象上,且![]() ,求
,求![]() 的取值范围(结果可用含m的式子表示).
的取值范围(结果可用含m的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
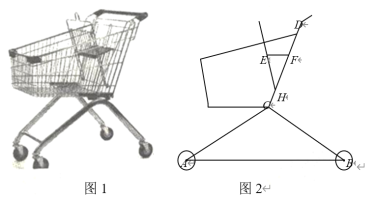
【题目】如图1是超市的手推车,如图2是其侧面示意图,已知前后车轮半径均为5 cm,两个车轮的圆心的连线AB与地面平行,测得支架AC=BC=60cm,AC、CD所在直线与地面的夹角分别为30°、60°,CD=50cm.
(1)求扶手前端D到地面的距离;
(2)手推车内装有简易宝宝椅,EF为小坐板,打开后,椅子的支点H到点C的距离为10 cm,DF=20cm,EF∥AB,∠EHD=45°,求坐板EF的宽度.(本题答案均保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
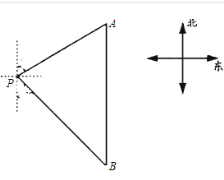
【题目】如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为100海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东37°方向上的B处,求此时轮船所在的B处与灯塔P的距离(sin53°=0.8,sin37°=0.6,tan53°=1.3,![]() 结果精确到0.1).
结果精确到0.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李明准备进行如下操作实验,把一根长40 cm的铁丝剪成两段,并把每段首尾相连各围成一个正方形.
(1)要使这两个正方形的面积之和等于58 cm2,李明应该怎么剪这根铁丝?
(2)李明认为这两个正方形的面积之和不可能等于48 cm2,你认为他的说法正确吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
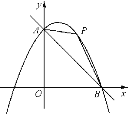
【题目】如图,直线![]() 与抛物线
与抛物线![]() 交于点A,B,点A在
交于点A,B,点A在![]() 轴上,点B在
轴上,点B在![]() 轴上.
轴上.
(1)求该抛物线的解析式.
(2)点P是直线AB上方的抛物线上的一动点,若S△AOB∶S△PAB=8∶3,求此时点P的坐标.
(3)点E是抛物线对称轴上的动点,点F是抛物线上的点,判断有几个位置能够使得点E,F,B,O为顶点的四边形是平行四边形,直接写出相应的点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知二次函数![]() .
.
(1)将![]() 化成
化成![]() 的形式为________;
的形式为________;
(2)此函数与![]() 轴的交点坐标为________;
轴的交点坐标为________;
(3)在平面直角坐标系![]() 中画出这个二次函数的图象(不用列表);
中画出这个二次函数的图象(不用列表);
(4)直接写出当![]() 时,
时,![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com