
【题目】下列正多边形中,与正三角形同时使用,能进行密铺的是( )
A.正十二边形
B.正十边形
C.正八边形
D.正五边形
科目:初中数学 来源: 题型:
【题目】老师想知道某校学生每天上学路上要花多少时间,于是随机选取30名同学每天来校的大致时间(单位:分钟)进行统计,统计表如下:
时间 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 45 |
人数 | 3 | 3 | 6 | 12 | 2 | 2 | 1 | 1 |
(1)写出这组数据的中位数和众数;
(2)求这30名同学每天上学的平均时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系xOy中,一次函数y=kx+2的图象与y轴交于点A,与x轴的正半轴交于点B,OA=2OB.
(1)直接写出点A、点B的坐标;
(2)在所给平面直角坐标系内画一次函数的图象. 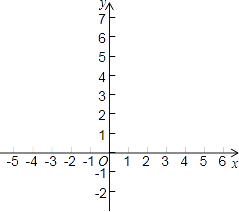
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题。
(1)如图①,△ABC中,点D、E在边BC上,AE平分∠BAC,AD⊥BC,∠C=40°,∠B=60°,求:①∠CAE的度数;②∠DAE的度数.
(2)如图②,若把(1)中的条件“AD⊥BC”变成“F为AE延长线上一点,且FD⊥BC”,其他条件不变,求出∠DFE的度数.
(3)在△ABC中,AE平分∠BAC,若F为EA延长线上一点,FD⊥BC,且∠C=α,∠B=β(β>α),试猜想∠DFE的度数(用α,β表示),请自己作出对应图形并说明理由. 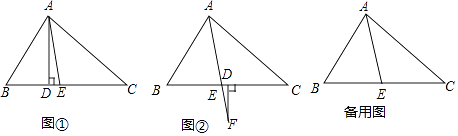
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,现有一张三角形ABC纸片,沿BC边上的高AE所在的直线翻折,使得点C与BC边上的点D重合.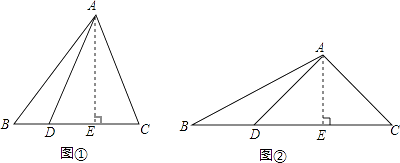
(1)填空:△ADC是三角形;
(2)若AB=15,AC=13,BC=14,求BC边上的高AE的长;
(3)如图②,若∠DAC=90°,试猜想:BC、BD、AE之间的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,对角线AC,BD相交于点O.
(1)如图1,点P是正方形ABCD外一点,连接OP,以OP为一边,作正方形OPMN,且边ON与边BC相交,连接AP,BN.
①依题意补全图1;
②判断AP与BN的数量关系及位置关系,写出结论并加以证明;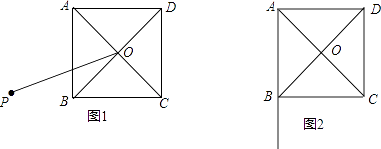
(2)点P在AB延长线上,且∠APO=30°,连接OP,以OP为一边,作正方形OPMN,且边ON与BC的延长线恰交于点N,连接CM,若AB=2,求CM的长(不必写出计算结果,简述求CM长的过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com