
【题目】如图,过原点O的直线与双曲线y=![]() 交于上A(m,n)、B,过点A的直线交x轴正半轴于点D,交y轴负半轴于点E,交双曲线y=
交于上A(m,n)、B,过点A的直线交x轴正半轴于点D,交y轴负半轴于点E,交双曲线y=![]() 于点P.
于点P.
(1)当m=2时,求n的值;
(2)当OD:OE=1:2,且m=3时,求点P的坐标;
(3)若AD=DE,连接BE,BP,求△PBE的面积.
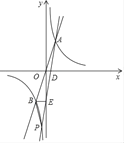
【答案】(1)3;(2)P(﹣2,﹣3);(3)3.
【解析】
(1)把A(2,n)代入解析式即可求出n;(2)先求出A点坐标,设OD=a,则OE=2a,得D(a,0),E(0,﹣2a),直线DE的解析式为y=2x﹣2a,把点A(3,2)代入求出a,再联立两函数即可求出交点P;(3)由AD=DE,点D在x轴坐标轴上,点E在y轴负半轴上,故A(m,n),E(0,﹣n),D(![]() m,0),求得直线DE的解析式为y=
m,0),求得直线DE的解析式为y=![]() x﹣n,又mn=6,得y=
x﹣n,又mn=6,得y=![]() x﹣n,与y=
x﹣n,与y=![]() 联立得
联立得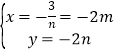 ,即为P点坐标,由直线AB的解析式为y=
,即为P点坐标,由直线AB的解析式为y=![]() x与双曲线联立解得B(﹣m,﹣n),再根据S△PBE=
x与双曲线联立解得B(﹣m,﹣n),再根据S△PBE=![]() BE×|yE﹣yP|=
BE×|yE﹣yP|=![]() ×m×|﹣n﹣(﹣2n)|求出等于3.
×m×|﹣n﹣(﹣2n)|求出等于3.
解:(1)∵点A(m,n)在双曲线y=![]() 上,
上,
∴mn=6,
∵m=2,
∴n=3;
(2)由(1)知,mn=6,
∵m=3,
∴n=2,
∴A(3,2),
∵OD:OE=1:2,
设OD=a,则OE=2a,
∵点D在x轴坐标轴上,点E在y轴负半轴上,
∴D(a,0),E(0,﹣2a),
∴直线DE的解析式为y=2x﹣2a,
∵点A(3,2)在直线y=2x﹣2a上,
∴6﹣2a=2,
∴a=2,
∴直线DE的解析式为y=2x﹣4①,
∵双曲线的解析式为y=![]() ②,
②,
联立①②解得,![]() (点A的横纵坐标,所以舍去)或
(点A的横纵坐标,所以舍去)或![]() ,
,
∴P(﹣2,﹣3);
(3)∵AD=DE,点D在x轴坐标轴上,点E在y轴负半轴上,A(m,n),
∴E(0,﹣n),D(![]() m,0),
m,0),
∴直线DE的解析式为y=![]() x﹣n,
x﹣n,
∵mn=6,
∴m=![]() ,
,
∴y=![]() x﹣n③,
x﹣n③,
∵双曲线的解析式为y=![]() ④,
④,
联立③④解得,
∴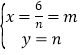 (点A的横纵坐标,所以舍去)或
(点A的横纵坐标,所以舍去)或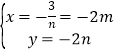 ,
,
∴P(﹣2m,﹣2n),
∵A(m,n),
∴直线AB的解析式为y=![]() x⑤.
x⑤.
联立④⑤解得,![]() (点A的横纵坐标,所以舍去)或
(点A的横纵坐标,所以舍去)或![]()
∴B(﹣m,﹣n),
∵E(0,﹣n),
∴BE∥x轴,
∴S△PBE=![]() BE×|yE﹣yP|=
BE×|yE﹣yP|=![]() ×m×|﹣n﹣(﹣2n)|=
×m×|﹣n﹣(﹣2n)|=![]() mn=3.
mn=3.


科目:初中数学 来源: 题型:
【题目】2018年首届“进博会”期间,上海对周边道路进行限速行驶.道路![]() 段为监测区,
段为监测区,![]() 、
、![]() 为监测点(如图).已知,
为监测点(如图).已知,![]() 、
、![]() 、
、![]() 在同一条直线上,且
在同一条直线上,且![]() ,
,![]() 米,
米,![]() ,
,![]() .
.
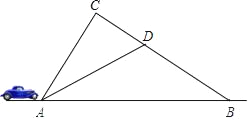
(1)求道路![]() 段的长;(精确到1米)
段的长;(精确到1米)
(2)如果![]() 段限速为60千米/时,一辆车通过
段限速为60千米/时,一辆车通过![]() 段的时间为90秒,请判断该车是否超速,并说明理由.(参考数据:
段的时间为90秒,请判断该车是否超速,并说明理由.(参考数据:![]()
![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,反比例函数y= ![]() 的图象与一次函数y=x+b的图象交
的图象与一次函数y=x+b的图象交
于点A(1,4)、点B(-4,n).

(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要在宽为22米的大道两边安装路灯,路灯的灯臂CD长2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,求路灯的灯柱BC高度.
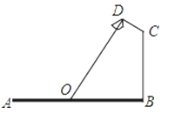
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲、乙两位运动员中选出一名参加在规定时间内的投篮比赛.预先对这两名运动员进行了6次测试,成绩如下(单位:个):
甲:6,12,8,12,10,12;
乙:9,10,11,10,12,8;
(1)填表:
平均数 | 众数 | 方差 | |
甲 | 10 |
|
|
乙 |
| 10 |
|
(2)根据测试成绩,请你运用所学的统计知识作出分析,派哪一位运动员参赛更好?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店老板去图书批发市场购买某种图书,第一次用1200元购书若干本,并按该书定价7元出售,很快售完.由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了20%,他用1500元所购该书的数量比第一次多10本,当按定价售出200本时,出现滞销,便以定价的4折售完剩余的书.
(1)第一次购书的进价是多少元?
(2)试问该老板这两次售书总体上是赔钱了,还是赚钱了(不考虑其他因素)?若赔钱,赔多少;若赚钱,赚多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中有两点![]() 、
、![]() ,我们定义
,我们定义![]() 、
、![]() 两点间的“
两点间的“![]() 值”直角距离为
值”直角距离为![]() ,且满足
,且满足![]() ,其中
,其中![]() .小静和佳佳在解决问题:(求点
.小静和佳佳在解决问题:(求点![]() 与点
与点![]() 的“1值”直角距离
的“1值”直角距离![]() )时,采用了两种不同的方法:
)时,采用了两种不同的方法:
(方法一):![]() ;
;
(方法二):如图1,过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作直线
作直线![]() 与
与![]() 轴交于点
轴交于点![]() ,则
,则![]()
请你参照以上两种方法,解决下列问题:
(1)已知点![]() ,点
,点![]() ,则
,则![]() 、
、![]() 两点间的“2值”直角距离
两点间的“2值”直角距离![]() .
.
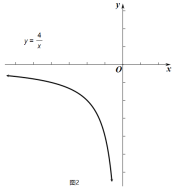
(2)函数![]() 的图像如图2所示,点
的图像如图2所示,点![]() 为其图像上一动点,满足
为其图像上一动点,满足![]() 两点间的“
两点间的“![]() 值”直角距离
值”直角距离![]() ,且符合条件的点
,且符合条件的点![]() 有且仅有一个,求出符合条件的“
有且仅有一个,求出符合条件的“![]() 值”和点
值”和点![]() 坐标.
坐标.
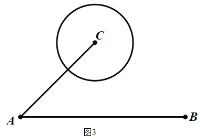
(3)城市的许多街道是相互垂直或平行的,因此,往往不能沿直线行走到达目的地,只能按直角拐弯的方式行走,因此,两地之间修建垂直和平行的街道常常转化为两点间的“![]() 值”直角距离,
值”直角距离,![]() 地位于
地位于![]() 地的正东方向上,
地的正东方向上,![]() 地在
地在![]() 点东北方向上且相距
点东北方向上且相距![]() ,以
,以![]() 为圆心修建了一个半径为
为圆心修建了一个半径为![]() 的圆形湿地公园,现在要在公园和
的圆形湿地公园,现在要在公园和![]() 地之间修建观光步道.步道只能东西或者南北走向,并且东西方向每千米成本是20万元,南北方向每千米的成本是10万元,问:修建这一规光步道至少要多少万元?
地之间修建观光步道.步道只能东西或者南北走向,并且东西方向每千米成本是20万元,南北方向每千米的成本是10万元,问:修建这一规光步道至少要多少万元?

查看答案和解析>>
科目:初中数学 来源: 题型:
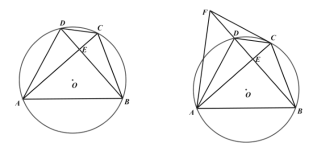
【题目】四边形![]() 是
是![]() 的内接四边形,
的内接四边形,![]() ,
,![]() ,垂足为
,垂足为![]() .
.
(1)如图1,求证:![]() ;
;
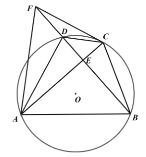
(2)如图2,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,连接
,连接![]() 、
、![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com