
【题目】如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A﹣C﹣B﹣A运动,设运动时间为t秒(t>0).
(1)若点P在AC上,且满足PA=PB时,求出此时t的值;
(2)若点P恰好在∠BAC的角平分线上,求t的值;
(3)在运动过程中,直接写出当t为何值时,△BCP为等腰三角形.
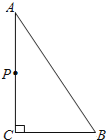
【答案】(1) ![]() ;(2)
;(2)![]() 或6;(3)当
或6;(3)当![]() 或
或![]() 时,△BCP为等腰三角形.
时,△BCP为等腰三角形.
【解析】
(1)设存在点P,使得![]() ,此时
,此时![]() ,
,![]() ,根据勾股定理列方程即可得到结论;
,根据勾股定理列方程即可得到结论;
(2)当点P在![]() 的平分线上时,如图1,过点P作
的平分线上时,如图1,过点P作![]() 于点E,此时
于点E,此时![]() ,
,![]() ,
,![]() ,根据勾股定理列方程即可得到结论;
,根据勾股定理列方程即可得到结论;
(3)在![]() 中,根据勾股定理得到
中,根据勾股定理得到![]() ,根据题意得:
,根据题意得:![]() ,当P在AC上时,
,当P在AC上时,![]() 为等腰三角形,得到
为等腰三角形,得到![]() ,即
,即![]() ,求得
,求得![]() ,当P在AB上时,
,当P在AB上时,![]() 为等腰三角形,若
为等腰三角形,若![]() ,点P在BC的垂直平分线上,如图2,过P作
,点P在BC的垂直平分线上,如图2,过P作![]() 于E,求得
于E,求得![]() ,若
,若![]() ,即
,即![]() ,解得
,解得![]() ,
,![]() ,如图3,过C作
,如图3,过C作![]() 于F,由射影定理得;
于F,由射影定理得;![]() ,列方程
,列方程![]() ,即可得到结论.
,即可得到结论.
解:在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
(1)设存在点P,使得![]() ,
,
此时![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
即:![]() ,
,
解得:![]() ,
,
![]() 当
当![]() 时,
时,![]() ;
;
(2)当点P在![]() 的平分线上时,如图1,过点P作
的平分线上时,如图1,过点P作![]() 于点E,
于点E,
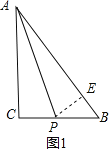
此时![]() ,
,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
即:![]() ,
,
解得:![]() ,
,
当![]() 时,点
时,点![]() 与
与![]() 重合,也符合条件,
重合,也符合条件,
![]() 当
当![]() 或6时,
或6时,![]() 在
在![]() 的角平分线上;
的角平分线上;
(3)根据题意得:![]() ,
,
当P在AC上时,![]() 为等腰三角形,
为等腰三角形,
![]() ,即
,即![]() ,
,
![]() ,
,
当P在AB上时,![]() 为等腰三角形,
为等腰三角形,
![]() ,点P在BC的垂直平分线上,
,点P在BC的垂直平分线上,
如图2,过P作![]() 于E,
于E,

![]() ,
,
![]() ,即
,即![]() ,解得:
,解得:![]() ,
,
![]() ,即
,即![]() ,
,
解得:![]() ,
,
![]() ,如图3,过C作
,如图3,过C作![]() 于F,
于F,
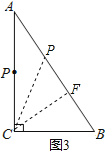
![]() ,
,
![]() ,
,
由射影定理得;![]() ,
,
即![]() ,
,
解得:![]() ,
,
![]() 当
当![]() 时,
时,![]() 为等腰三角形.
为等腰三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,点D是AB边的中点,点E为AC中点,点F在边BC上,AF交DE于点G,点H是FC的中点,连接GH.

(1)如图1,求证:四边形GHCE是平行四边形;
(2)如图2,当AB=AC,点F是BC中点时,在不添加任何辅助线的情况下,请直接写出图中所有长度等于![]() BF的线段.
BF的线段.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学活动课上,某校初三数学老师带领学生去测河宽,如图所示,某学生在河东岸点![]() 处观测到河对岸水边有一点
处观测到河对岸水边有一点![]() ,测得
,测得![]() 在
在![]() 北偏西
北偏西![]() 的方向上,沿河岸向北前行20米到达
的方向上,沿河岸向北前行20米到达![]() 处,测得
处,测得![]() 在
在![]() 北偏西
北偏西![]() 的方向上,请你根据以上数据,帮助该同学计算出这条河的宽度.(参考数值:tan31°≈
的方向上,请你根据以上数据,帮助该同学计算出这条河的宽度.(参考数值:tan31°≈![]() ,sin31°≈
,sin31°≈![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列一组方程:①![]() ,②
,②![]() ,③
,③![]() ,…小明通过观察,发现了其中蕴含的规律,并顺利地求出了前三个方程的解第①个方程的解为
,…小明通过观察,发现了其中蕴含的规律,并顺利地求出了前三个方程的解第①个方程的解为![]() ;第②个方程的解为
;第②个方程的解为![]() ;第③个方程的解为
;第③个方程的解为![]() .若n为正整数,且关于x的方程
.若n为正整数,且关于x的方程![]() 的一个解是
的一个解是![]() ,则n的值等于____________.
,则n的值等于____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解
如图1,![]() 中,沿
中,沿![]() 的平分线
的平分线![]() 折叠,剪掉重叠部分;将余下部分沿
折叠,剪掉重叠部分;将余下部分沿![]() 的平分线
的平分线![]() 折叠,剪掉重叠部分;……;将余下部分沿
折叠,剪掉重叠部分;……;将余下部分沿![]() 的平分线
的平分线![]() 折叠,点
折叠,点![]() 与点
与点![]() 重合,无论折叠多少次,只要最后一次恰好重合,我们就称
重合,无论折叠多少次,只要最后一次恰好重合,我们就称![]() 是
是![]() 的好角.
的好角.
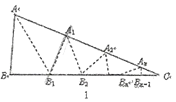
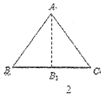
情形一:如图2,沿等腰三角形![]() 顶角
顶角![]() 的平分线
的平分线![]() 折叠,点
折叠,点![]() 与点
与点![]() 重合;
重合;
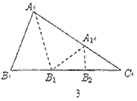
情形二:如图3,沿![]() 的
的![]() 的平分线
的平分线![]() 折叠,剪掉重叠部分;将余下的部分沿
折叠,剪掉重叠部分;将余下的部分沿![]() 的平分线
的平分线![]() 折叠,此时点
折叠,此时点![]() 与点
与点![]() 重合.
重合.
探究发现
(1)![]() 中,
中,![]() ,经过两次折叠,问
,经过两次折叠,问![]()
![]() 的好角(填写“是”或“不是”);
的好角(填写“是”或“不是”);
(2)若经过三次折叠发现![]() 是
是![]() 的好角,请探究
的好角,请探究![]() 与
与![]() (假设
(假设![]() )之间的等量关系 ;
)之间的等量关系 ;
根据以上内容猜想:若经过![]() 次折叠
次折叠![]() 是
是![]() 的好角,则
的好角,则![]() 与
与![]() (假设
(假设![]() )之间的等量关系为 ;
)之间的等量关系为 ;
应用提升:
(3)小丽找到一个三角形,三个角分别为![]() ,
,![]() ,
,![]() ,发现 是此三角形的好角;
,发现 是此三角形的好角;
(4)如果一个三角形的最小角是![]() ,且满足该三角形的三个角均是此三角形的好角;
,且满足该三角形的三个角均是此三角形的好角;
则此三角形另外两个角的度数 .
查看答案和解析>>
科目:初中数学 来源: 题型:
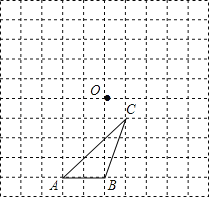
【题目】如图所示,△ABC与点O在10×10的网格中的位置如图所示
(1)画出△ABC绕点O逆时针旋转90°后的图形;
(2)画出△ABC绕点O逆时针旋转180°后的图形;
(3)若⊙M能盖住△ABC,则⊙M的半径最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在同一平面内,将△ABC绕A点逆时针旋转到△ADE的位置.若AC⊥DE,∠ABD=62°,则∠ACB的度数为( )

A.56°B.44°C.34°D.40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC.以AB为直径的⊙O分别与BC、AC相交于点D、E,连接AD.过点D作DF⊥AC,垂足为点F,
(1)求证:DF是⊙O的切线;
(2)若⊙O的半径为4,∠CDF=22.5°,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B,有人在直线AB上点C(靠点B一侧)竖直向上摆放若干个无盖的圆柱形桶.试图让网球落入桶内,已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).当竖直摆放圆柱形桶至少( )个时,网球可以落入桶内.

A.7B.8C.9D.10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com