
【题目】某商店用2500元采购A型商品的件数是用750元采购B种商品件数数量的2倍,已知一件A型商品的进价比一件B型商品的进价多10元.
(1)求一件A,B型商品的进价分别为多少元?
(2)若商店购进A,B型商品共150件,已知A型商品的售价为30元/件,B型商品的售价为25元/件,且全部售出,设购进A型商品m件,求这批商品的利润W(元)与m之间的函数关系式;
(3)在(2)的条件下,若A型商品的件数不少于B型商品的4倍,请你设计获利最大的进货方案,并求最大利润.
【答案】(1)一件A型商品的进价为25元,一件B型商品的进价为15元;(2)W=-5m+1500;(3)获利最大进货方案为A型商品采购120件,B型商品采购30件,最大利润为900元.
【解析】
(1)根据题意可以列出相应的分式方程,从而可求得一件A、B型商品的进价分别为多少元,注意分式方程要检验;
(2)根据“利润![]() (售价
(售价![]() 进价)
进价)![]() 件数”即可得出W与m的函数关系式;
件数”即可得出W与m的函数关系式;
(3)先求出m的取值范围,再根据一次函数的性质即可求出最大利润.
(1)设一件B型商品的进价为x元,则一件A型商品的进价为![]() 元
元
由题意得![]()
解得![]()
经检验,![]() 是原分式方程的解
是原分式方程的解
此时,![]()
答:一件A型商品的进价为25元,一件B型商品的进价为15元;
(2)由题意和(1)的结论得:![]()
答:这批商品的利润W(元)与m之间的函数关系式是![]() ;
;
(3)∵A型商品的件数不少于B型商品的4倍
∴![]()
解得![]()
又∵![]()
解得![]()
∴![]()
∵![]() ,
,![]()
∴W随m的增大而减小
∴当![]() 时,W取得最大值,最大值为
时,W取得最大值,最大值为![]() (元)
(元)
此时,![]() (元)
(元)
答:获利最大进货方案为A型商品采购120件,B型商品采购30件,最大利润为900元.


科目:初中数学 来源: 题型:
【题目】学校广播站要招聘一名播音员,擅长诵读的小龙想去应聘,但是不知道是否符合应聘条件,于是在微信上向好朋友亮亮倾诉,如图所示的是他们的部分对话内容,面对小龙的问题,亮亮也犯了难.
(1)请聪明的你用所学的方程知识帮小龙计算一下,他是否符合学校广播站的应聘条件?
(2)小龙和奶奶各读一篇文章,已知奶奶所读文章比小龙所读文章至少多了3200个字,但奶奶所用的时间是小龙的2倍,则小龙至少读了多少分钟?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店将每件进价为80元的某种商店按每件110元出售,每天可售出100件.该商店想通过降低售价、增加销售量的方法来提高利润.经市场调查,发现这种商品每件每降价5元,每天的销售量可增加50件.设商品降价x元,每天销售该商品获得的利润为y元.
(1)求y(元)关于x(元)的函数关系式,并写出x的取值范围.
(2)求当x取何值时y最大?并求出y的最大值.
(3)若要是每天销售利润为3750元,且尽可能最大的向顾客让利,应将该商品降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦BC=2cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发沿着A→B→A方向运动,设运动时间为t(s)(0≤t<3),连接EF,当△BEF是直角三角形时,t(s)的值为【 】

A.![]() B.1 C.
B.1 C.![]() 或1 D.
或1 D.![]() 或1或
或1或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两人以相同路线前往距离单位10km的培训中心参加学习,图中1,![]() 分别表示甲、乙两人前往目的地所走的路程S(千米)随时间(分)变化的函数图象,以下说法:①甲比乙提前12分钟到达;②甲的平均速度为15千米/小时;③甲、乙相遇时,乙走了6千米;④乙出发6分钟后追上甲,其中正确的是( )
分别表示甲、乙两人前往目的地所走的路程S(千米)随时间(分)变化的函数图象,以下说法:①甲比乙提前12分钟到达;②甲的平均速度为15千米/小时;③甲、乙相遇时,乙走了6千米;④乙出发6分钟后追上甲,其中正确的是( )
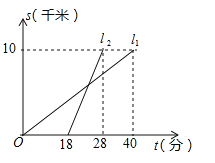
A.①②B.③④C.①③④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老张匀速开车从A市送货到B市,途中汽车出现小故障,老张只能降速为原速的一半行驶等待B市的修车师傅小李前往修车,半小时后,小李与老张相遇,立马开始修车,车修好后,老张又提速为原速的![]() 继续开车送货到B市,小李以原速返回B市,老张和小李距离B市的路程y(千米)与老张出发的时间x(小时)的函数图象分别如图所示(途中其它损耗时间忽略不计),则小李在返回到B市时,老张距B市______千米.
继续开车送货到B市,小李以原速返回B市,老张和小李距离B市的路程y(千米)与老张出发的时间x(小时)的函数图象分别如图所示(途中其它损耗时间忽略不计),则小李在返回到B市时,老张距B市______千米.
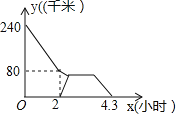
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国很多城市水资源缺乏,为了加强居民的节水意识,某市制定了每月用水4吨以内(包括4吨)和用水4吨以上收费标准(收费标准:每吨水的价格)某用户每月应交水费y(元)与用水量x(吨)之间关系的图象如图:
(1)说出自来水公司在这两个用水范围内的收费标准;
(2)当x>4时,求因变量y与自变量x之间的关系式;
(3)若某用户该月交水费26元,求他用了多少吨水?
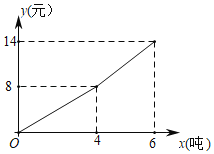
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
(1)请画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
(2)请画出△ABC绕点B逆时针旋转90°后的△A2BC2;
(3)求出(2)中C点旋转到C2点所经过的路径长(结果保留根号和π);
(4)求出(2)△A2BC2的面积是多少.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com