【题目】如图，在平面直角坐标系中，将坐标原点沿轴向左平移个单位长度得到点，过点作轴的平行线交反比例函数的图象于点，.

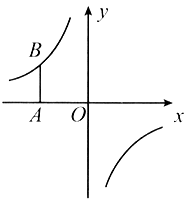
（1）求反比例函数的解析式；

（2）若、是该反比例函数图象上的两点，且时，，指出点、各位于哪个象限？并简要说明理由．

【题目】如图，E、F在线段BC上，AB=DC，AE=DF，BF=CE，以下结论是否正确？请说明理由．

（1）∠B=∠C；
（2）AF∥DE．

（1）在一次数学活动中，某小组学生将菱形的一边与平行四边形较短边重合，摆拼成如图1所示的图形，经过点，连接交于点，观察发现：点是的中点．

下面是两位学生有代表性的证明思路：

思路１：不需作辅助线，直接证三角形全等；

思路2：不证三角形全等，连接交于点．、

……

请参考上面的思路，证明点是的中点（只需用一种方法证明）；

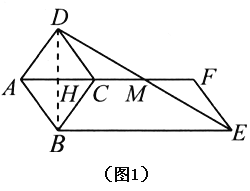
（2）如图2，在（1）的条件下，当时，延长、交于点，求的值；

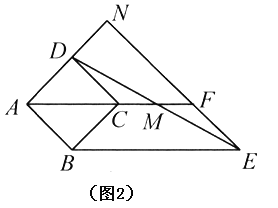
（3）在（2）的条件下，若（为大于的常数），直接用含的代数式表示的值．

【题目】在平面直角坐标系中，我们定义直线为抛物线（、、为常数，）的“梦想直线”；有一个顶点在抛物线上，另一个顶点在轴上的三角形为其“梦想三角形”．

已知抛物线与其“梦想直线”交于、两点（点在点的左侧），与轴负半轴交于点．

（1）填空：该抛物线的“梦想直线”的解析式为 ，点的坐标为 ，点的坐标为 ；

（2）如图，点为线段上一动点，将以所在直线为对称轴翻折，点的对称点为，若为该抛物线的“梦想三角形”，求点的坐标；

（3）当点在抛物线的对称轴上运动时，在该抛物线的“梦想直线”上，是否存在点，使得以点、、、为顶点的四边形为平行四边形？若存在，请直接写出点、的坐标；若不存在，请说明理由．

【题目】如图，D是△ABC的BC边上的一点，∠B =40°，∠ADC=80°．

（1）求证：AD=BD；
（2）若∠BAC=70°，判断△ABC的形状，并说明理由．

①a，b，c是直线，若a∥b，b∥c，则a∥c．

②a，b，c是直线，若a⊥b，b⊥c，则a⊥c．

③若∠α与∠β互余，∠β与∠γ互余，则∠α与∠γ互余．

其中正确的命题是（　　）

A.①B.①②C.②③D.①②③