
科目: 来源: 题型:
【题目】把几个图形拼成一个新的图形,再通过图形面积的计算,常常可以得到一些有用的信息,或可以求出一些不规则图形的面积.
(1)如图1所示,将一张长方形纸板按图中虚线裁剪成九块,其中有两块是边长都为m的大正方形,两块是边长都为n的小正方形,五块是长为m,宽为n的全等小长方形,且m>n.观察图形,可以发现代数式2m2+5mn+2n2可以因式分解为 .
(2)若图1中每块小长方形的面积为12cm2,四个正方形的面积和为50 cm2,试求图中所有裁剪线(虚线部分)长之和.
(3)将图2中边长为a和b的正方形拼在一起,B,C,G三点在同一条直线上,连接BD和BF,若这两个正方形的边长满足a+b=10,ab=16,请求出阴影部分的面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】共享单车作为一种低碳、时尚、绿色的出行方式,它俨然成为市民出行的“新宠”.某公司准备安装A款共享单车,完成5760辆该款共享单车投入市场运营的计划.由于抽调不出足够的熟练工人完成安装,公司准备招聘一批新工人,将他们培训到能独立进行安装后上岗。生产开始后发现:4名熟练工人和5名新工人每天共安装88辆共享单车;2名熟练工人每天安装的共享单车数与3名新工人每天安装的共享单车数一样多.
(1)求每名熟练工人和新工人每天分别可以安装多少辆共享单车?
(2)若公司招聘m名新工人,使得招聘的新工人和抽调的熟练工人刚好一个月(30天)完成安装任务,已知工人们安装的共享单车中不能正常投入运营的占4%,且招聘的新工人数比抽调的熟练工人数少,求m的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示的暗礁区,两灯塔A,B之间的距离恰好等于圆的半径,为了使航船(S)不进入暗礁区,那么S对两灯塔A,B的视角∠ASB必须( ) 
A.大于60°
B.小于60°
C.大于30°
D.小于30°
查看答案和解析>>
科目: 来源: 题型:
【题目】我们在计算(2+1)(22+1)(24+1)(28+1)(216+1)时,发现直接运算很麻烦,如果在算式前乘以(2-1),即1,原算式的值不变,而且还使整个算式是能用乘法公式计算.
即:原式=(2-1) (2+1)(22+1)(24+1)(28+1)(216+1)=232-1.
请用上述方法算出(5+1) (52+1)(54+1)(58+1)(516+1) (532+1)的值为_________.
查看答案和解析>>
科目: 来源: 题型:
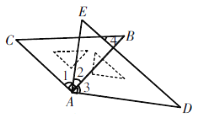
【题目】将一副三角板按如图放置,则下列结论:
①如果∠2=30°,则有AC∥DE;
②∠BAE+∠CAD =180°;
③如果BC∥AD,则有∠2=45°;
④如果∠CAD=150°,必有∠4=∠C;
正确的有( )
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目: 来源: 题型:
【题目】已知如图,矩形OABC的长OA= ![]() ,宽OC=1,将△AOC沿AC翻折得△APC.
,宽OC=1,将△AOC沿AC翻折得△APC.
(1)求∠PCB的度数;
(2)若P,A两点在抛物线y=﹣ ![]() x2+bx+c上,求b,c的值,并说明点C在此抛物线上;
x2+bx+c上,求b,c的值,并说明点C在此抛物线上;
(3)(2)中的抛物线与矩形OABC边CB相交于点D,与x轴相交于另外一点E,若点M是x轴上的点,N是y轴上的点,以点E、M、D、N为顶点的四边形是平行四边形,试求点M、N的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列多项式的乘法中,能用平方差公式计算的是( )
A. (-m +n)(m - n) B. (![]() a +b)(b -
a +b)(b -![]() a)
a)
C. (x + 5)(x + 5) D. (3a -4b)(3b +4a)
查看答案和解析>>
科目: 来源: 题型:
【题目】问题:有甲、乙、丙三种商品,①购甲3件、乙5件、丙7件共需490元钱;②购甲4件、乙7件、丙10件共需690元钱;③购甲2件,乙3件,丙1件共需170元钱. 求购甲、乙、丙三种商品各一件共需多少元?
小明说:“可以根据3个条件列出三元一次方程组,分别求出购甲、乙、丙一件需多少钱,再相加即可求得答案.”
小丽经过一番思考后,说:“本题可以去掉条件③,只用①②两个条件,仍能求出答案.” 针对小丽的发言,同学们进行了热烈地讨论.
(1)请你按小明的思路解决问题.
(2)小丽的说法正确吗?如果正确,请完成解答过程;如果不正确,请说明理由.
(3)请根据上述解决问题中积累的经验,解决下面的问题:学校购买四种教学用具A、B、C、D,第一次购A教具1件、B教具3件、 C教具4件、D教具5件共花2018元;第二次购A教具1件、B教具5件、 C教具7件、D教具9件共花3036元. 求购A教具5件、B教具3件、 C教具2件、D教具1件共需多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】某电器商场销售A、B两种型号计算器,两种计算器的进货价格分别为每台30元、40元. 商场销售5台A型号和1台B型号计算器,可获利润76元;销售6台A型号和3台B型号计算器,可获利润120元.
(1)求商场销售A、B两种型号计算器的销售价格分别是多少元?(利润=销售价格﹣进货价格)
(2)商场准备用不多于2500元的资金购进A、B两种型号计算器共70台,问最少需要购进A型号的计算器多少台?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com