【题目】如图，已知四边形ABCD内接于⊙O，直径AC=6，对角线AC、BD交于E点，且AB=BD，EC=1，则AD的长为（ ）
A.
B.
C.
D.3

【题目】如图，在ABCD中，对角线AC、BD交于点O，并且∠DAC=60°，∠ADB=15°．点E是AD边上一动点，延长EO交BC于点F．当点E从D点向A点移动过程中（点E与点D，A不重合），则四边形AFCE的变化是（ ）
A.平行四边形→矩形→平行四边形→菱形→平行四边形
B.平行四边形→菱形→平行四边形→矩形→平行四边形
C.平行四边形→矩形→平行四边形→正方形→平行四边形
D.平行四边形→矩形→菱形→正方形→平行四边形

【题目】如图，抛物线y=ax2+bx+2与直线l交于点A、B两点，且A点为抛物线与y轴的交点，B（﹣2，﹣4），抛物线的对称轴是直线x=2，过点A作AC⊥AB，交抛物线于点C、x轴于点D．

（1）求此抛物线的解析式；
（2）求点D的坐标；
（3）抛物线上是否存在点K，使得以AC为边的平行四边形ACKL的面积等于△ABC的面积？若存在，请直接写出点K的横坐标；若不存在，请说明理由．[提示：抛物线y=ax2+bx+c（a≠0）的对称轴为x=﹣ ，顶点坐标为（﹣ ， ）]．

（1）请画出△ABC沿x轴向右平移3个单位长度,再沿y轴向上平移2个单位长度后的△A′B′C′（其中A′、B′、C′分别是A、B、C的对应点，不写画法）

（2）直接写出A′、B′、C′三点的坐标：

A′（___________）； B′（___________）；C′（___________）。

（3）求△ABC的面积。

（1）从火车站到码头怎样走最近，画图并说明理由；

（2）从码头到铁路怎样走最近，画图并说明理由；

（3）从火车站到河流怎样走最近，画图并说明理由．

【题目】如图，已知⊙O是以BC为直径的△ABC的外接圆，OP∥AC，且与BC的垂线交于点P，OP交AB于点D，BC、PA的延长线交于点E．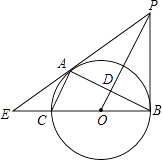
（1）求证：PA是⊙O的切线；
（2）若sinE= ，PA=6，求AC的长．

【题目】某商家到梧州市一茶厂购买茶叶，购买茶叶数量为x千克（x＞0），总费用为y元，现有两种购买方式． 方式一：若商家赞助厂家建设费11500元，则所购茶叶价格为130元/千克；（总费用=赞助厂家建设费+购买茶叶费）
方式二：总费用y（元）与购买茶叶数量x（千克）满足下列关系式：y= ．
请回答下面问题：
（1）写出购买方式一的y与x的函数关系式；
（2）如果购买茶叶超过150千克，说明选择哪种方式购买更省钱；
（3）甲商家采用方式一购买，乙商家采用方式二购买，两商家共购买茶叶400千克，总费用共计74600元，求乙商家购买茶叶多少千克？

（1）当A，B，C三点在同一直线上时（如图1），求证：M为AN的中点；

（2）将图1中△BCE绕点B旋转，当A，B，E三点在同一直线上时（如图2），求证：△CAN为等腰直角三角形；

（3）将图1中△BCE绕点B旋转到图3的位置时，(2)中的结论是否仍然成立？若成立，试证明之；若不成立，请说明理由．