
科目: 来源: 题型:
【题目】如图,已知点A(﹣m,n),B(0,m),且m、n满足![]() +(n﹣5)2=0,点C在y轴上,将△ABC沿y轴折叠,使点A落在点D处.
+(n﹣5)2=0,点C在y轴上,将△ABC沿y轴折叠,使点A落在点D处.

(1)写出D点坐标并求A、D两点间的距离;
(2)若EF平分∠AED,若∠ACF﹣∠AEF=20°,求∠EFB的度数;
(3)过点C作QH平行于AB交x轴于点H,点Q在HC的延长线上,AB交x轴于点R,CP、RP分别平分∠BCQ和∠ARX,当点C在y轴上运动时,∠CPR的度数是否发生变化?若不变,求其度数;若变化,求其变化范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1是一种包装盒的表面展开图,将它围起来可得到一个几何体的模型.
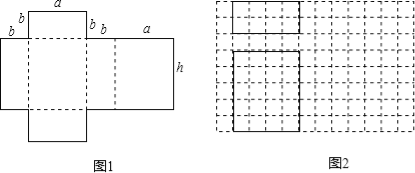
(1)这个几何体模型的名称是 .
(2)如图2是根据a,b,h的取值画出的几何体的主视图和俯视图(图中实线表示的长方形),请在网格中画出该几何体的左视图.
(3)若h=a+b,且a,b满足![]() a2+b2﹣a﹣6b+10=0,求该几何体的表面积.
a2+b2﹣a﹣6b+10=0,求该几何体的表面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】“一带一路”让中国和世界更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯.如图1所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒2度,灯B转动的速度是每秒1度.假定主道路是平行的,即PQ∥MN,且∠BAM:∠BAN=2:1.
(1)填空:∠BAN=_____°;
(2)若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?
(3)如图2,若两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作∠ACD交PQ于点D,且∠ACD=120°,则在转动过程中,请探究∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.

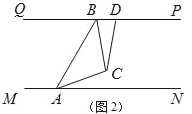
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读材料后解决问题:
小明遇到下面一个问题:
计算(2+1)(22+1)(24+1)(28+1).
经过观察,小明发现如果将原式进行适当的变形后可以出现特殊的结构,进而可以应用平方差公式解决问题,具体解法如下:(2+1)(22+1)(24+1)(28+1)
=(2+1)(2﹣1)(22+1)(24+1)(28+1)
=(22﹣1)(22+1)(24+1)(28+1)
=(24﹣1)(24+1)(28+1)
=(28﹣1)(28+1)
=216﹣1
请你根据小明解决问题的方法,试着解决以下的问题:
(1)(2+1)(22+1)(24+1)(28+1)(216+1)=_____.
(2)(3+1)(32+1)(34+1)(38+1)(316+1)=_____.
(3)化简:(m+n)(m2+n2)(m4+n4)(m8+n8)(m16+n16).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知点A(﹣1,0),B(4,0),点C在y轴的正半轴上,且∠ACB=90°,抛物线y=ax2+bx+c经过A、B、C三点,其顶点为M.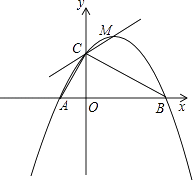
(1)求抛物线y=ax2+bx+c的解析式;
(2)试判断直线CM与以AB为直径的圆的位置关系,并加以证明;
(3)在抛物线上是否存在点N,使得S△BCN=4?如果存在,那么这样的点有几个?如果不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】江海化工厂计划生产甲、乙两种季节性产品,在春季中,甲种产品售价50千元/件,乙种产品售价30千元/件,生产这两种产品需要A、B两种原料,生产甲产品需要A种原料4吨/件,B种原料2吨/件,生产乙产品需要A种原料3吨/件,B种原料1吨/件,每个季节该厂能获得A种原料120吨,B种原料50吨.
(1)如何安排生产,才能恰好使两种原料全部用完?此时总产值是多少万元?
(2)在夏季中甲种产品售价上涨10%,而乙种产品下降10%,并且要求甲种产品比乙种产品多生产25件,问如何安排甲、乙两种产品,使总产值是1375千元,A,B两种原料还剩下多少吨?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com