
科目: 来源: 题型:
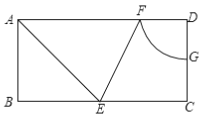
【题目】如图,矩形ABCD中,BC=2AB=4,AE平分∠BAD交边BC于点E,∠AEC的分线交AD于点F,以点D为圆心,DF为半径画圆弧交边CD于点G,求FG的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点A、B的坐标分别为A(-4,0)、B(2,0),点C在y轴上,且△ABC的面积为6,以点A、B、C为顶点作□ABCD.若过原点的直线平分该□ABCD的面积,则此直线的解析式是________.
查看答案和解析>>
科目: 来源: 题型:
【题目】下面的说法正确的是( )
A.有理数的绝对值一定比0大
B.有理数的相反数一定比0小
C.如果两个数的绝对值相等,那么这两个数相等
D.互为相反数的两个数的绝对值相等
查看答案和解析>>
科目: 来源: 题型:
【题目】某食品厂生产的一种巧克力糖每千克成本为24元,其销售方案有如下两种:
方案一:若直接给本厂设在银川的门市部销售,则每千克售价为32元,但门市部每月需上缴有关费用2400元;
方案二:若直接批发给本地超市销售,则出厂价为每千克28元.若每月只能按一种方案销售,且每种方案都能按月销售完当月产品,设该厂每月的销售量为xkg.
(1)你若是厂长,应如何选择销售方案,可使工厂当月所获利润更大?
(2)厂长看到会计送来的第一季度销售量与利润关系的报表后(下表),发现该表填写的销售量与实际有不符之处,请找出不符之处,并计算第一季度的实际销售总量.
一月 | 二月 | 三月 | |
销售量(kg) | 550 | 600 | 1400 |
利润(元) | 2000 | 2400 | 5600 |
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校给“希望小学”邮寄每册a元的图书240册,若每册图书的邮费为书价的5%,则共需邮费()
A.5%a元B.240a(1+5%)元
C.5%×240a元D.240元
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面材料:随着人们认识的不断深入,毕达哥拉斯学派逐渐承认![]() 不是有理数,并给出了证明.假设是
不是有理数,并给出了证明.假设是![]() 有理数,那么存在两个互质的正整数p,q,使得
有理数,那么存在两个互质的正整数p,q,使得![]() ,于是
,于是![]() ,两边平方得p2=2q2 . 因为2q2是偶数,所以p2是偶数,而只有偶数的平方才是偶数,所以p也是偶数.因此可设p=2s,代入上式,得4s2=2q2 , 即q2=2s2 , 所以q也是偶数,这样,p和q都是偶数,不互质,这与假设p,q互质矛盾,这个矛盾说明,
,两边平方得p2=2q2 . 因为2q2是偶数,所以p2是偶数,而只有偶数的平方才是偶数,所以p也是偶数.因此可设p=2s,代入上式,得4s2=2q2 , 即q2=2s2 , 所以q也是偶数,这样,p和q都是偶数,不互质,这与假设p,q互质矛盾,这个矛盾说明, ![]() 不能写成分数的形式,即
不能写成分数的形式,即![]() 不是有理数.请你有类似的方法,证明
不是有理数.请你有类似的方法,证明![]() 不是有理数.
不是有理数.
查看答案和解析>>
科目: 来源: 题型:
【题目】【再现】如图①,在△ABC中,点D,E分别是AB,AC的中点,可以得到:DE∥BC,且DE=![]() BC.(不需要证明)
BC.(不需要证明)
【探究】如图②,在四边形ABCD中,点E,F,G,H分别是AB,BC,CD,DA的中点,判断四边形EFGH的形状,并加以证明.
【应用】在(1)【探究】的条件下,四边形ABCD中,满足什么条件时,四边形EFGH是菱形?你添加的条件是: .(只添加一个条件)
(2)如图③,在四边形ABCD中,点E,F,G,H分别是AB,BC,CD,DA的中点,对角线AC,BD相交于点O.若AO=OC,四边形ABCD面积为5,则阴影部分图形的面积和为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com