
科目: 来源: 题型:
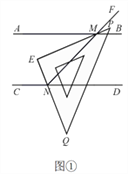
【题目】已知,点![]() 是线段
是线段![]() 所在平面内任意一点,分别以
所在平面内任意一点,分别以![]() 、
、![]() 为边,在
为边,在![]() 同侧作等边
同侧作等边![]() 和等边
和等边![]() ,联结
,联结![]() 、
、![]() 交于点
交于点![]() .
.
(1)如图1,当点![]() 在线段
在线段![]() 上移动时,线段
上移动时,线段![]() 与
与![]() 的数量关系是:________;
的数量关系是:________;
(2)如图2,当点![]() 在直线
在直线![]() 外,且
外,且![]() ,仍分别以
,仍分别以![]() 、
、![]() 为边,在
为边,在![]() 同侧作等边
同侧作等边![]() 和等边
和等边![]() ,联结
,联结![]() 、
、![]() 交于点
交于点![]() .(1)的结论是否还存在?若成立,请证明;若不成立,请说明理由.此时
.(1)的结论是否还存在?若成立,请证明;若不成立,请说明理由.此时![]() 是否随
是否随![]() 的大小发生变化?若变化,写出变化规律,若不变,请求出
的大小发生变化?若变化,写出变化规律,若不变,请求出![]() 的度数;
的度数;
(3)如图3,在(2)的条件下,联结![]() ,求证:
,求证: ![]() 平分
平分![]() .
.

查看答案和解析>>
科目: 来源: 题型:
【题目】我国出租车的收费标准因地而异,济宁市规定:起步价为6元,3千米之后每千米1.4元;济南市规定:起步价8元,3千米之后每千米1.2元.
(1)求济宁的李先生乘出租车2千米,5千米应付的车费;
(2)写出在济宁乘出租车行x千米时应付的车费;
(3)当行驶路程超过3千米,不超过l3千米时,求在济南、济宁两地坐出租车的车费相差多少?
(4)如果李先生在济南和济宁乘出租车所付的车费相等,试估算出李先生乘出租车多少千米(直接写出答案,不必写过程).
查看答案和解析>>
科目: 来源: 题型:
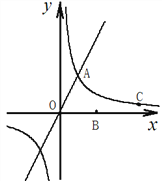
【题目】如图,正比例函数![]() (
(![]() )的图像与反比例函数
)的图像与反比例函数![]() (
(![]() )的图像交于点
)的图像交于点![]() ,且点
,且点![]() 在反比例函数的图像上,点
在反比例函数的图像上,点![]() 的坐标为
的坐标为![]() .
.
(1)求正比例函数![]() 的解析式;
的解析式;
(2)若![]() 为射线
为射线![]() 上一点,①若点
上一点,①若点![]() 的横坐标为
的横坐标为![]() ,
, ![]() 的面积为
的面积为![]() ,写出
,写出![]() 关于
关于![]() 的函数解析式,并指出自变量
的函数解析式,并指出自变量![]() 的取值范围;②当
的取值范围;②当![]() 是等腰三角形时,求点
是等腰三角形时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】王老师家买了一套新房,其结构如图所示(单位:m).他打算将卧室铺上木地板,其余部分铺上地砖.
(1)木地板和地砖分别需要多少平方米?
(2)如果地砖的价格为每平方米x元,木地板的价格为每平方米3x元,那么王老师需要花多少钱?

查看答案和解析>>
科目: 来源: 题型:
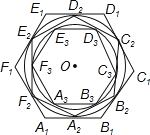
【题目】如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A10B10C10D10E10F10的边长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数y=ax2-5x+c的图象如图所示,请根据图象回答下列问题:
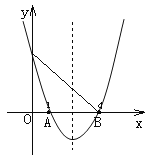
(1) a=_______,c=______.
(2)函数图象的对称轴是_________,顶点坐标P__________.
(3)该函数有最______值,当x=______时,y最值=________.
(4)当x_____时,y随x的增大而减小.当x_____时,y随x的增大而增大.
(5)抛物线与x轴交点坐标A_______,B________;与y轴交点C 的坐标为_______;![]() =_________,
=_________,![]() =________.
=________.
(6)当y>0时,x的取值范围是_________;当y<0时,x的取值范围是_________.
(7)方程ax2-5x+c=0中△的符号为________.方程ax2-5x+c=0的两根分别为_____,____.
(8)当x=6时,y______0;当x=-2时,y______0.
查看答案和解析>>
科目: 来源: 题型:
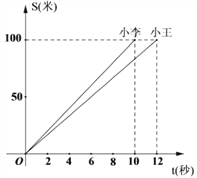
【题目】如图,是小王和小李在一次跑步比赛中的时间和路程图.
(1)这次比赛的路程是_______米;
(2)小王的平均速度是_________米/秒;
(3)他们先到达终点的是_______;
(4)小李跑步的路程![]() (米)与时间
(米)与时间![]() (秒)的函数关系式是_________.
(秒)的函数关系式是_________.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知: 两直线![]() ,
,![]() ,且
,且![]() ∥CD,点
∥CD,点![]() ,
,![]() 分别在直线
分别在直线![]() ,
,![]() 上. 放置一个足够大的三角尺,使得三角尺的两边
上. 放置一个足够大的三角尺,使得三角尺的两边![]() ,
,![]() 分别经过点
分别经过点![]() ,
,![]() . 过点
. 过点![]() 作射线
作射线![]() ,使得
,使得![]() .
.
(1)转动三角尺,如图①所示,当射线![]() 与
与![]() 重合,
重合,![]() 时,则
时,则![]() ________;
________;
(2)转动三角尺,如图②所示,当射线![]() 与
与![]() 不重合,
不重合,![]() 时,求
时,求![]() 的度数.
的度数.
(3)转动直角三角尺的过程中, 请直接写出![]() 与
与![]() 之间的数量关系.
之间的数量关系.


查看答案和解析>>
科目: 来源: 题型:
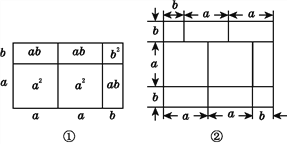
【题目】先阅读再解答:我们已经知道,根据几何图形的面积关系可以说明完全平方公式,实际上还有一些等式也可以用这种方式加以说明,例如:
(2a+b)(a+b)=2a2+3ab+b2,就可以用图①的面积关系来说明.
(1)根据图②写出一个等式: ;
(2)已知等式:(x+p)(x+q)=x2+(p+q)x+pq,请你画出一个相应的几何图形加以说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com