
科目: 来源: 题型:
【题目】在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证( )

A. (a+b)2=a2+2ab+b2
B. (a﹣b)2=a2﹣2ab+b2
C. a2﹣b2=(a+b)(a﹣b)
D. (a+2b)(a﹣b)=a2+ab﹣2b2
查看答案和解析>>
科目: 来源: 题型:
【题目】如图.从下列四个条件:①BC=B′C,②AC=A′C,③∠A′CA=∠B′CB,④AB=A′B′中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目: 来源: 题型:
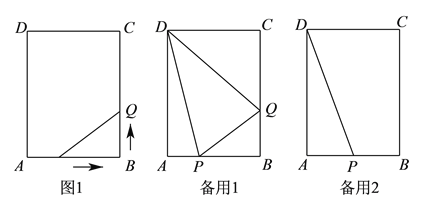
【题目】如图![]() ,在长方形
,在长方形![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 从点
从点![]() 开始以
开始以![]() 的速度沿
的速度沿![]() 边向点
边向点![]() 运动,点
运动,点![]() 从点
从点![]() 以
以![]() 的速度沿
的速度沿![]() 边向点
边向点![]() 运动,如果
运动,如果![]() 、
、![]() 同时出发,设运动时间为
同时出发,设运动时间为![]() .
.
(![]() )当
)当![]() 时,求
时,求![]() 的长.
的长.
(![]() )当点
)当点![]() 运动到点
运动到点![]() 时,
时, ![]() 、
、![]() 同时停止运动.在运动过程中,是否存在
同时停止运动.在运动过程中,是否存在![]() 的值,使得
的值,使得![]() 、
、![]() 、
、![]() 的面积都相等,若存在,求出
的面积都相等,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(![]() )当运动
)当运动![]() 时,
时, ![]() 点停止运动,
点停止运动, ![]() 点以原速立即向
点以原速立即向![]() 点返回,在返回的过程中,
点返回,在返回的过程中, ![]() 是否能平分
是否能平分![]() ?若能,求出点
?若能,求出点![]() 运动的时间;若不能,请说明理由.
运动的时间;若不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某校7年级的学生从学校O点出发,要到某地P处进行探险活动,他们先向正西方向走8km到A处,又往正南方向走4km到B处,又折向正东方向走6km到C处,再折向正北方向走8km到D处,最后又往正东方向走4km才到探险地P;取点O为原点,取点O的正东方向为x轴的正方向,取点O的正北方向为y轴的正方向,以2km为一个单位长度建立平面直角坐标系.

(1)在平面直角坐标系中画出探险路线图;
(2)分别写出A、B、C、D、P点的坐标.
查看答案和解析>>
科目: 来源: 题型:
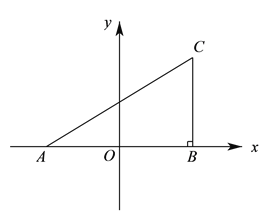
【题目】如图①,在平面直角坐标系中, ![]() ,
, ![]() ,且满足
,且满足![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() .
.
(![]() )求
)求![]() 的面积.
的面积.
(![]() )在
)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 和
和![]() 的面积相等?若存在,求出
的面积相等?若存在,求出![]() 点坐标;若不存在,说明理由.
点坐标;若不存在,说明理由.
(![]() )动点
)动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 的速度沿射线
的速度沿射线![]() 运动,如果在运动过程中
运动,如果在运动过程中![]() 为等腰三角形,求出点
为等腰三角形,求出点![]() 运动的时间.
运动的时间.
查看答案和解析>>
科目: 来源: 题型:
【题目】实验与探究:
(![]() )如图,直线
)如图,直线![]() 为第一、三象限的角平分线,观察易知
为第一、三象限的角平分线,观察易知![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 的坐标为
的坐标为![]() ,请在图中分别标明
,请在图中分别标明![]() 、
、![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 、
、![]() 的位置,并写出他们的坐标:
的位置,并写出他们的坐标: ![]() __________、
__________、![]() __________.
__________.
(![]() )结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点
)结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点![]() 关于第一、三象限的角平分线
关于第一、三象限的角平分线![]() 的对称点
的对称点![]() 的坐标为__________ (不必证明).
的坐标为__________ (不必证明).
(![]() )已知两点
)已知两点![]() 、
、![]() ,在直线
,在直线![]() 上是否存在一点
上是否存在一点![]() ,使点
,使点![]() 到
到![]() 、
、![]() 两点的距离之和最小,并求出最小距离.
两点的距离之和最小,并求出最小距离.

查看答案和解析>>
科目: 来源: 题型:
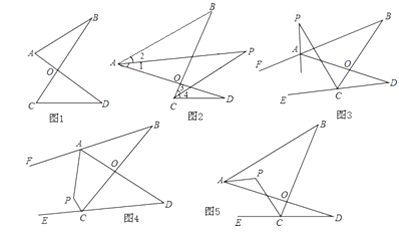
【题目】根据题意解答:(1)如图1的图形我们把它称为“8字形”,请说明∠A+∠B=∠C+∠D.
(2)阅读下面的内容,并解决后面的问题: 如图2,AP、CP分别平分∠BAD、∠BCD,若∠ABC=36°,∠ADC=16°,求∠P的度数.
解:∵AP、CP分别平分∠BAD、∠BCD
∴∠1=∠2,∠3=∠4
由(1)的结论得:∠P+∠3=∠1+∠B①,∠P+∠2=∠4+∠D②,①+②,得2∠P+∠2+∠3=∠1+∠4+∠B+∠D
∴∠P= ![]() (∠B+∠D)=26°.
(∠B+∠D)=26°.
①如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,请猜想∠P的度数,并说明理由.
②在图4中,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论,无需说明理由.
③在图5中,AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论,无需说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】端午节前夕,小东的父母准备购买若干个粽子和咸鸭蛋(每个粽子的价格相同,每个咸鸭蛋的价格相同).已知粽子的价格比咸鸭蛋的价格贵1.8元,花30元购买粽子的个数与花12元购买咸鸭蛋的个数相同,求粽子与咸鸭蛋的价格各多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)在图 (每个小正方形的边长均为1)中建立两个不同的平面直角坐标系,在各个坐标系中分别写出六边形6个顶点的坐标;
(2)要使图中点B与点F的横坐标互为相反数,则应选取怎样的直线作为y轴,试在图中标出来,此时点E与点C的横坐标有什么关系?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com