（1）把△ABC向下平移8个单位后得到对应的△A1B1C1，画出△A1B1C1；

（2）画出与△A1B1C1关于y轴对称的△A2B2C2；

（3）若点P（a，b）是△ABC边上任意一点，P2是△A2B2C2边上与P对应的点，写出P2的坐标为　 　 ；

（4）试在y轴上找一点Q(在图中标出来)，使得点Q到B2、C2两点的距离之和最小，并求出QB2+QC2的最小值．

填空：① ∠AEB的度数为_______；②线段AD、BE之间的数量关系是______．

（2）拓展研究：

如图2，△ACB和△DCE均为等腰三角形，且∠ACB=∠DCE=90°，点A、D、E在同一直线上，若AE=15，DE=7，求AB的长度．

（3）探究发现：

图1中的△ACB和△DCE，在△DCE旋转过程中当点A，D，E不在同一直线上时，设直线AD与BE相交于点O，试在备用图中探索∠AOE的度数，直接写出结果，不必说明理由．

已知：如图1，l1∥l2∥l3，点A、M、B分别在直线l1，l2，l3上，MC平分∠AMB，∠1=28°，∠2=70°．求：∠CMD的度数．

小明想了许久没有思路，就去请教好朋友小坚，小坚给了他如图2所示的提示：

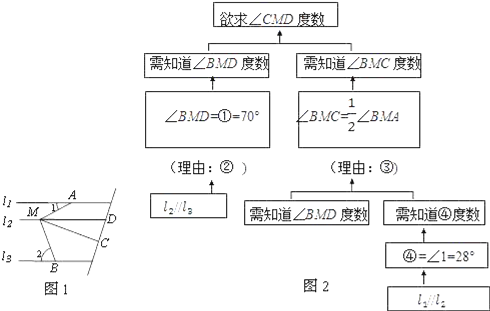
请问小坚的提示中①是∠　 　，④是∠　 　．

理由②是：　 　；

理由③是：　 　；

∠CMD的度数是　 　°．

【题目】如图，平面直角坐标系中，直线AB： 交y轴于点A，交x轴于点B，过点E(2，0)作x轴的垂线EF交AB于点D，点P是垂线EF上一点，且S△ADP=2，以PB为边在第一象限作等腰Rt△BPC，则点C的坐标为_________．

A．0.2或0.3

B．0.4

C．0.3

D．0.2

A. 0．36πm2 B. 0．81πm2 C. 2πm2 D. 3.24πm2

(1)筹委会计划，购买书刊的资金不少于购买书桌、书架等设施资金的3倍，问最多用多少资金购买书桌、书架等设施？

(2)经初步统计，有200户居民自愿参与集资，那么平均每户需集资150元．镇政府了解情况后，赠送了一批阅览室设施和书籍，这样，只需参与户共集资20 000元．经筹委会进一步宣传，自愿参与的户数在200户的基础上增加了a%(其中a>0)．则每户平均集资的资金在150元的基础上减少了a%，求a的值.

【题目】已知一次函数y＝kx＋7的图像经过点A（2，3）．

（1）求k的值；

（2）判断点B（－1，8），C（3，1）是否在这个函数的图像上，并说明理由；

（3）当－3＜x＜－1时，求y的取值范围．

【答案】（1）k=-2（2）点B不在，点C在，（3）9＜y＜13

【解析】

试题分析：（1）把点A（2，3）代入y＝kx＋7即可求出k的值；（2）点B（－1，8），C（3，1）的横坐标代入函数解析式验证即可；（3）根据x的取值范围，即可求出y的取值范围．

试题解析：（1）把点A（2，3）代入y＝kx＋7得：k=-2

（2）当x=-1时，y=-2×（-1）+7=9

∵9≠8∴点B不在抛物线上．

当x=3时，y=-2×3+7=1

∴点C在抛物线上

（3）当x=-3时，y=13，当x=-,1时，y=9，所以9＜y＜13

考点：一次函数．

【题型】解答题
【结束】
24

（1）分别计算甲、乙两车的速度及a的值；

（2）乙车到达B地后以原速立即返回，请问甲车到达B地后以多大的速度立即匀速返回，才能与乙车同时回到A地？并在图中画出甲、乙两车在返回过程中离A地的距离S（km）与时间t（h）的函数图象．

【题目】如图，在所给正方形网格（每个小网格的边长是1）图中完成下列各题.

（1）格点△ABC（顶点均在格点上）的面积=_________；

（2）画出格点△ABC关于直线DE对称的△A1B1C1；

（3）在DE上画出点P，使PB+PC最小，并求出这个最小值．

【答案】（1）面积等于5（2）图形见解析（3）最小值是根号17

【解析】试题分析：(1)利用勾股定理求出三角形边长，并证明是直角三角形求面积.(2)画出A，B，C的对称点A1,B2,C3，连接三角形.(3)利用对称利用两点之间直线最短求最小值.

试题解析：

（1）分别利用勾股定理求得AC=2,AB=,BC=， ,所以∠ACB=90°，面积等于=5.

（2）画出A，B，C的对称点A1,B2,C3，连接三角形.如下图.

（3）作B点对称B’,连接B’C交DE于P,B’P+PC=BP+CP,所以使PB+PC最小.

利用勾股定理B’C=，

所以最小值是根号17.

点睛：平面上最短路径问题

（1）归于“两点之间的连线中，线段最短”.凡属于求“变动的两线段之和的最小值”时，大都应用这一模型.

（2）归于“三角形两边之差小于第三边”.凡属于求“变动的两线段之差的最大值”时，大都应用这一模型.

（3）平面图形中，直线同侧两点到直线上一点距离之和最短问题.

【题型】解答题
【结束】
23

（1）求k的值；

（2）判断点B（－1，8），C（3，1）是否在这个函数的图像上，并说明理由；

（3）当－3＜x＜－1时，求y的取值范围．