A. ∠2=∠3 B. ∠l=∠3 C. ∠4+∠5=180 D. ∠2=∠4

【题目】如图,在平行四边形OABC中,已知点A、C两点的坐标为A (,),C (2,0).

(1)求点B的坐标.

(2)将平行四边形OABC向左平移个单位长度,求所得四边形A′B′C′O′四个顶点的坐标.

(3)求平行四边形OABC的面积.

【题目】如图，在△ABC中，∠ACB=90°，分别以点A和B为圆心，以相同的长（大于 AB）为半径作弧，两弧相交于点M和N，作直线MN交AB于点D，交BC于点E，连接CD，下列结论错误的是（ ）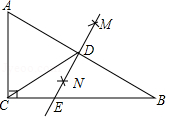
A.AD=BD
B.BD=CD
C.∠A=∠BED
D.∠ECD=∠EDC

（1）两同学向公司经理了解租车的价格，公司经理对他们说：“公司有45座和60座两种型号的客车可供租用，60座的客车每辆每天的租金比45座的贵100元．”王老师说：“我们学校八年级昨天在这个公司租了5辆45座和2辆60座的客车，一天的租金为1600元，你们能知道45座和60座的客车每辆每天的租金各是多少元吗”甲、乙两同学想了一下，都说知道了价格．

聪明的你知道45座和60座的客车每辆每天的租金各是多少元吗？

（2）公司经理问：“你们准备怎样租车”，甲同学说：“我的方案是只租用45座的客车，可是会有一辆客车空出30个座位”；乙同学说“我的方案只租用60座客车，正好坐满且比甲同学的方案少用两辆客车”，王老师在﹣旁听了他们的谈话说：“从经济角度考虑，还有别的方案吗”？如果是你，你该如何设计租车方案，并说明理由．

(1)

(2) ．

【题目】如图，Rt△OAB如图所示放置在平面直角坐标系中，直角边OA与x轴重合，∠OAB=90°，OA=4，AB=2，把Rt△OAB绕点O逆时针旋转90°，点B旋转到点C的位置，一条抛物线正好经过点O，C，A三点．

（1）求该抛物线的解析式；
（2）在x轴上方的抛物线上有一动点P，过点P作x轴的平行线交抛物线于点M，分别过点P，点M作x轴的垂线，交x轴于E，F两点，问：四边形PEFM的周长是否有最大值？如果有，请求出最值，并写出解答过程；如果没有，请说明理由．
（3）如果x轴上有一动点H，在抛物线上是否存在点N，使O（原点）、C、H、N四点构成以OC为一边的平行四边形？若存在，求出N点的坐标；若不存在，请说明理由．

请将下面的解答过程补充完整，并填空（理由或数学式）

解：∵DE∥BC，∴∠DEF= ．（　　）

∵EF∥AB，∴ =∠ABC．（　　）

∴∠DEF=∠ABC．（等量代换）

∵∠ABC=40°，∴∠DEF= °．

（2）应用：如图②，直线AB、BC、AC两两相交，交点分别为点A、B、C，点D在线段AB的延长线上，过点D作DE∥BC交AC于点E，过点E作EF∥AB交BC于点F．若∠ABC=60°，则∠DEF= °．

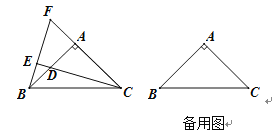
（1）点D在边AB上时，试探究线段BD、AB和AF的数量关系，并证明你的结论；

（2）点D在AB的延长线或反向延长线上时，（1）中的结论是否成立？若不成立，请直接写出正确结论.

（1）求证：△ABE≌△CBF；

（2）若∠CAE=30°，求∠ACF的度数．