
科目: 来源: 题型:
【题目】甲、乙两位同学本学年每个单元的测验成绩如下(单位:分):
甲:98,100,100,90,96,91,89,99,100,100,93
乙:98,99,96,94,95,92,92,98,96,99,97
(1)、他们的平均成绩分别是多少?
(2)、甲、乙的11次单元测验成绩的标准差分别是多少?
(3)、这两位同学的成绩各有什么特点?
(4)、现要从中选出一人参加“希望杯”竞赛,历届比赛成绩表明,平时成绩达到98分以上才可能进入决赛,你认为应选谁参加这项竞赛,为什么?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )

A. 76° B. 78° C. 80° D. 82°
查看答案和解析>>
科目: 来源: 题型:
【题目】(7分)某省现在正处于50年不遇的干旱.某中学八年级(2班)共50名同学,开展了“献爱心”捐款活动,活动结束后,班长将捐款情况进行了统计,并绘制成了如图所示的统计图.

(1)求50名同学的捐款平均数.
(2)该中学共有学生2000名,请根据该班的捐款情况,估计这所中学的捐款数.
查看答案和解析>>
科目: 来源: 题型:
【题目】希望中学八年级学生开展踢毽子活动,每班派5名学生参加,按团体总分排列名次,在规定时间内每人踢100个以上(含100)为优秀.下表是成绩较好的甲班和乙班5名学生的比赛成绩(单位:个)
1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
甲班 | 100 | 98 | 110 | 89 | 103 | 500 |
乙班 | 89 | 100 | 95 | 119 | 97 | 500 |
经统计发现两班5名学生踢毽子的总个数相等.此时有学生建议,可以通过考查数据中的其它信息作为参考.请你回答下列问题:
(1)求两班比赛数据的中位数;
(2)计算两班比赛数据的方差,并比较哪一个小;
(3)根据以上信息,你认为应该把冠军奖状发给哪一个班?简述理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在数轴上点A表示数a,点B表示数b,AB表示A点和B点之间的距离,且a,b满足|a+2|+(b+3a)2=0.
(1)求A,B两点之间的距离;
(2)若在线段AB上存在一点C,且AC=2BC,求C点表示的数;
(3)若在原点O处放一个挡板,一小球甲从点A处以1个单位/秒的速度向左运动,同时,另一个小球乙从点B处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略小球的大小,可看做一个点)以原来的速度向相反的方向运动.
设运动时间为t秒.
①甲球到原点的距离为_____,乙球到原点的距离为_________;(用含t的代数式表示)
②求甲乙两小球到原点距离相等时经历的时间.
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】(7分)某学校举行演讲比赛,选出了10名同学担任评委,并事先拟定从如下4个方案中选择合理的方案来确定每个演讲者的最后得分(满分为10分):
方案1:所有评委所给分的平均数,
方案2:在所有评委所给分中,去掉一个最高分和一个最低分.然后再计算其余给分的l平均数.
方案3:所有评委所给分的中位效.
方案4:所有评委所给分的众数.
为了探究上述方案的合理性.先对某个同学的演讲成绩进行了统计实验.下面是这个同学的得分统计图:

(1)分别按上述4个方案计算这个同学演讲的最后得分;
(2)根据(1)中的结果,请用统计的知识说明哪些方案不适台作为这个同学演讲的最后得分,并给出该同学的最后得分.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图①,直线y= ![]() x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
(1)求抛物线F1所表示的二次函数的表达式;
(2)若点M是抛物线F1位于第二象限图象上的一点,设四边形MAOC和△BOC的面积分别为S四边形MAOC和S△BOC , 记S=S四边形MAOC﹣S△BOC , 求S最大时点M的坐标及S的最大值;
(3)如图②,将抛物线F1沿y轴翻折并“复制”得到抛物线F2 , 点A、B与(2)中所求的点M的对应点分别为A′、B′、M′,过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D、P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
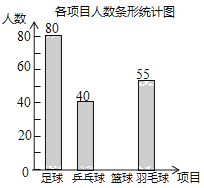
【题目】某学校准备开展“阳光体育活动”,决定开设以下体育活动项目:足球、乒乓球、篮球和羽毛球,要求每位学生必须且只能选择一项,为了解选择各种体育活动项目的学生人数,随机抽取了部分学生进行调查,并将通过获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据统计图回答问题:
(1)这次活动一共调查了 名学生;
(2)补全条形统计图;
(3)在扇形统计图中,选择篮球项目的人数所在扇形的圆心角等于 度;
(4)若该学校有1500人,请你估计该学校选择足球项目的学生人数约是 人。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com