
科目: 来源: 题型:
【题目】(1)操作实践:△ABC中,∠A=90°,∠B=22.5°,请画出一条直线把△ABC分割成两个等腰三角形,并标出分割成两个等腰三角形底角的度数;(要求用两种不同的分割方法)
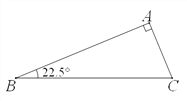
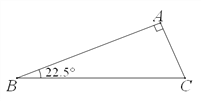
(2)分类探究:△ABC中,最小内角∠B=24°,若△ABC被一直线分割成两个等腰三角形,请画出相应示意图并写出△ABC最大内角的所有可能值;
(3)猜想发现:若一个三角形能被一直线分割成两个等腰三角形,需满足什么条件?(请你至少写出两个条件,无需证明)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在△ABC中,∠BAC=75°,∠ACB=35°,∠ABC的平分线BD交边AC于点D.
(1)求证:△BCD为等腰三角形;
(2)若∠BAC的平分线AE交边BC于点E,如图2,求证:BD+AD=AB+BE;
(3)若∠BAC外角的平分线AE交CB延长线于点E,请你探究(2)中的结论是否仍然成立?直接写出正确的结论.


图1 图2
查看答案和解析>>
科目: 来源: 题型:
【题目】为保护环境,我市公交公司计划购买A型和B型两种环保节能公交车共10辆.若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在某线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次,则该公司有哪几种购车方案?
(3)在(2)的条件下,哪种购车方案总费用最少?最少总费用是多少万元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,锐角△ABC中,∠ACB=30°,AB=5,△ABC的面积为23.
(1)若点P在AB边上且CP=![]() ,D,E分别为边AC,BC上的动点.求△PDE周长的最小值;
,D,E分别为边AC,BC上的动点.求△PDE周长的最小值;
(2)假设一只小羊在△ABC区域内,从路边AB某点出发跑到水沟边AC喝水,然后跑向路边BC吃草,再跑回出发点处休息,直接写出小羊所跑的最短路程.

查看答案和解析>>
科目: 来源: 题型:
【题目】我们知道对于一个图形,通过不同的方法计算图形的面积可以得到一个数学等式.
例如:由图1可得到(a+b)=a+2ab+b.
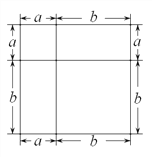
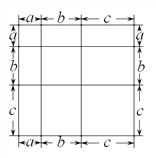
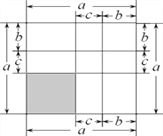
图1 图2 图3
(1)写出由图2所表示的数学等式:_____________________;写出由图3所表示的数学等式:_____________________;
(2)利用上述结论,解决下面问题:已知a+b+c=11,bc+ac+ab=38,求a+b+c的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=![]() ∠CAB.
∠CAB.
(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠CBF=![]() , 求BC和BF的长.
, 求BC和BF的长.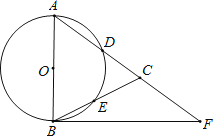
查看答案和解析>>
科目: 来源: 题型:
【题目】特值验证:
当![]() ,0,1,2,5,…时,计算代数式
,0,1,2,5,…时,计算代数式![]() 的值,分别得到5,2,1,2,17,….当x的取值发生变化时,代数式
的值,分别得到5,2,1,2,17,….当x的取值发生变化时,代数式![]() 的值却有一个确定的范围,通过多次验证可以发现它的值总大于或等于1,所以1就是它的最小值.
的值却有一个确定的范围,通过多次验证可以发现它的值总大于或等于1,所以1就是它的最小值.
变式求证:
我们可以用学过的知识,对![]() 进行恒等变形:
进行恒等变形:![]() .(注:这种变形方法可称为“配方”)
.(注:这种变形方法可称为“配方”) ![]() ,
,![]() .所以无论x取何值,代数式
.所以无论x取何值,代数式![]() 的值不小于1,即最小值为1.
的值不小于1,即最小值为1.
迁移实证:
(1)请你用“配方”的方法,确定![]() 的最小值为3;
的最小值为3;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】△ABC中,∠A=90°,AB=AC , BC=63cm,现沿底边依次从下往上裁剪宽度均为3cm的矩形纸条,如图所示,已知剪得的纸条中有一张是正方形,则这张正方形纸条是从下往上数第张.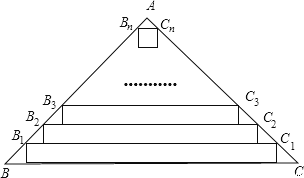
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com