科目： 来源： 题型：
【题目】在△ABC中，∠A，∠B，∠C的对应边分别是a，b，c，则满足下列条件但不是直角三角形的是（ ）
A. ∠A=∠B-∠C B. ∠A：∠B：∠C=1：3：4 C. a：b：c=1：
：3 D. 
查看答案和解析>>
科目： 来源： 题型：
【题目】如图是2017年杭州市某月24日08时至25日07时的空气质量指数统计图(空气质量指数AQI的值在不同的区间，就代表了不同的空气质量水平．比如0～50之间，代表“良好”，对应的颜色为绿色；51～100之间，代表“中等”，对应的颜色为黄色；101～150之间，代表“对敏感人群不健康”，对应的颜色为橙色，等等)，则根据统计图得出的下列判断，正确的是( )
A. 在这个24小时中，AQI的值超过良好限值时段是24日08时至24日12时
B. 在这个24小时中，AQI对应的颜色为黄色的时段持续了20小时以上
C. 在这个24小时中，AQI的最大值和最小值的差为77
D. 建议中老年朋友在25日06时至07时进行晨练
查看答案和解析>>
科目： 来源： 题型：
【题目】如图，ABCD是矩形纸片，翻折∠B，∠D，使AD，BC边与对角线AC重叠，且顶点B，D恰好落在同一点O上，折痕分别是CE，AF，则
等于（ ）
A. 
B. 2 C. 1.5 D. 
查看答案和解析>>
科目： 来源： 题型：
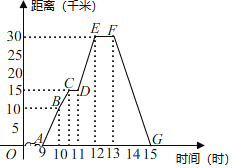
【题目】如图所示表示王勇同学骑自行车离家的距离与时间之间的关系，王勇9点离开家，15点回家，请结合图象，回答下列问题：
到达离家最远的地方是什么时间？离家多远？
他一共休息了几次？休息时间最长的一次是多长时间？
在哪些时间段内，他骑车的速度最快？最快速度是多少？
查看答案和解析>>
科目： 来源： 题型：
【题目】在一个不透明的口袋里装有仅颜色不同的黑、白两种颜色的球20只，某学习小组做摸球实验．将球搅匀后从中随机摸出一个球，记下颜色，再把它放回袋中，不断重复，下表是活动进行中记下的一组数据
摸球的次数 | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数 | 58 | 96 | 116 | 295 | 484 | 601 |
摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
（1）请你估计，当n很大时，摸到白球的频率将会接近 （精确到0.1）．
（2）假如你去摸一次，你摸到白球的概率是 ，摸到黑球的概率是 ．
（3）试估算口袋中黑、白两种颜色的球有多少只．
查看答案和解析>>
科目： 来源： 题型：
【题目】如图，在平面直角坐标系中，O为坐标原点，点A的坐标为（﹣8，0），直线BC经过点B（﹣8，6），C（0，6），将四边形OABC绕点O按顺时针方向旋转角度α得到四边形OA′B′C′，此时边OA′与边BC交于点P，边B′C′与BC的延长线交于点Q，连接AP．
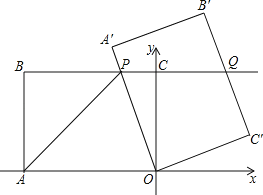
（1）四边形OABC的形状是 ．
（2）在旋转过程中，当∠PAO=∠POA，求P点坐标．
（3）在旋转过程中，当P为线段BQ中点时，连接OQ，求△OPQ的面积．
查看答案和解析>>
科目： 来源： 题型：
【题目】已知有理数a、b在数轴上的对应点如图所示．
（1）已知a=–2.3，b=0.4，计算|a+b|–|a|–|1–b|的值；
（2）已知有理数a、b，计算|a+b|–|a|–|1–b|的值．
查看答案和解析>>
科目： 来源： 题型：
【题目】已知如图，直线EF与AB、CD分别相交于点E、F．
（1）如图1，若∠1=120°，∠2=60°，求证AB∥CD；
（2）在（1）的情况下，若点P是平面内的一个动点，连结PE、PF，探索∠EPF、∠PEB、∠PFD三个角之间的关系；
①当点P在图2的位置时，可得∠EPF=∠PEB+∠PFD；
请阅读下面的解答过程，并填空（理由或数学式）
解：如图2，过点P作MN∥AB，
则∠EPM=∠PEB_____．
∵AB∥CD（已知），MN∥AB（作图）
∴MN∥CD_____．
∴∠MPF=∠PFD
∴∠_____+∠_____=∠PEB+∠PFD（等式的性质）
即∠EPF=∠PEB+∠PFD
②当点P在图3的位置时，∠EPF、∠PEB、∠PFD三个角之间有何关系并证明．
③当点P在图4的位置时，请直接写出∠EPF、∠PEB、∠PFD三个角之间的关系：_____．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
