
科目: 来源: 题型:
【题目】如图是同一时刻学校里一棵树和旗杆的影子,如果树高为3米,测得它的影子长为1.2米,旗杆的高度为5米,则它的影子长为( ) 
A.4米
B.2米
C.1.8米
D.3.6米
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,抛物线y=ax2+bx+3(a≠0)与x轴、y轴分别交于点A(﹣1,0)、B(3,0)、点C三点.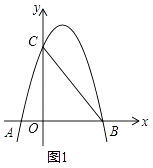
(1)试求抛物线的解析式;
(2)点D(2,m)在第一象限的抛物线上,连接BC,BD.试问,在对称轴左侧的抛物线上是否存在一点P,满足∠PBC=∠DBC?如果存在,请求出点P点的坐标;如果不存在,请说明理由;
(3)如图2,在(2)的条件下,将△BOC沿x轴正方向以每秒1个单位长度的速度向右平移,记平移后的三角形为△B′O′C′.在平移过程中,△B′O′C′与△BCD重叠的面积记为S,设平移的时间为t秒,试求S与t之间的函数关系式?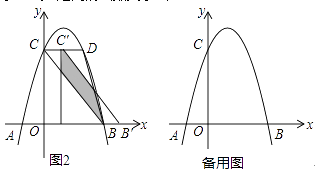
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,是若干个粗细均匀的铁环最大限度的拉伸组成的链条,已知铁环粗0.5厘米,每个铁环长4.6厘米,设铁环间处于最大限度的拉伸状态
(1)填表:
铁环个数 | 1 | 2 | 3 | 4 |
链条长(cm) | 4.6 | 8.2 | _____ | ____ |
(2)设n个铁环长为y厘米,请用含n的式子表示y;
(3)若要组成2.17米长的链条,至少需要多少个铁环?
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图某商场为了吸引顾客,设立了一个可以自由转动的转盘,并规定:每购买500元商品,就能获得一次转动转盘的机会,如果转盘停止后,指针上对准500、20、100、50、10的区域,顾客就可以分别获得500元、200元、100元、50元、10元的购物券一张。(转盘等分成20份)

(1)小华购物450元,他获得购物券的概率是多少?
(2)小丽购物600元,那么她获得100元以上(包括100元)券的概率是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,Rt△ABC中,∠BAC=90°,AB=AC=2,BC=![]() .点D从B点开始运动到C点结束(点D和B、C均不重合),DE交AC于E,∠ADE=45°,当△ADE是等腰三角形时,AE的长度为__________.
.点D从B点开始运动到C点结束(点D和B、C均不重合),DE交AC于E,∠ADE=45°,当△ADE是等腰三角形时,AE的长度为__________.
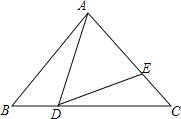
查看答案和解析>>
科目: 来源: 题型:
【题目】在Rt△ABC中,BC=AC,∠ACB=90°,点D为射线AB上一点,连接CD,过点C作线段CD的垂线l,在直线l上,分别在点C的两侧截取与线段CD相等的线段CE和CF,连接AE、BF.
(1)当点D在线段AB上时(点D不与点A、B重合),如图1
①请你将图形补充完整;
②线段BF、AD所在直线的位置关系为 ,线段BF、AD的数量关系为 ;
(2)当点D在线段AB的延长线上时,如图2
①请你将图形补充完整;
②在(1)中②问的结论是否仍然成立?如果成立请进行证明,如果不成立,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】著名的瑞士数学家欧拉曾指出:可以表示为四个整数平方之和的甲、乙两数相乘,其乘积仍然可以表示为四个整数平方之和,即![]()
![]() ,这就是著名的欧拉恒等式,有人称这样的数为“不变心的数”.实际上,上述结论可减弱为:可以表示为两个整数平方之和的甲、乙两数相乘,其乘积仍然可以表示为两个整数平方之和.
,这就是著名的欧拉恒等式,有人称这样的数为“不变心的数”.实际上,上述结论可减弱为:可以表示为两个整数平方之和的甲、乙两数相乘,其乘积仍然可以表示为两个整数平方之和.
【动手一试】
试将![]() 改成两个整数平方之和的形式.
改成两个整数平方之和的形式. ![]() ;
;
【阅读思考】
在数学思想中,有种解题技巧称之为“无中生有”.例如问题:将代数式![]() 改成两个平方之差的形式.解:原式
改成两个平方之差的形式.解:原式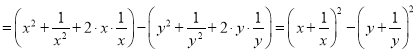 ﹒
﹒
【解决问题】
请你灵活运用利用上述思想来解决“不变心的数”问题:将代数式![]() 改成两个整数平方之和的形式(其中a、b、c、d均为整数),并给出详细的推导过程﹒
改成两个整数平方之和的形式(其中a、b、c、d均为整数),并给出详细的推导过程﹒
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AD为∠CAF的角平分线,BD=CD,∠DBC=∠DCB,∠DCA=∠ABD,过D作DE⊥AC于E,DF⊥AB交BA的延长线于F,则下列结论:①△CDE≌△BDF;②CE=AB+AE;③∠BDC=∠BAC;④∠DAF=∠CBD.其中正确的结论有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面材料:
学习了三角形全等的判定方法(即“SAS”“ASA”“AAS”“SSS”)和直角三角形全等的判定方法(即“HL”)后,小聪继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究
小聪将命题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E.
小聪的探究方法是对∠B分为“直角、钝角、锐角”三种情况进行探究.
第一种情况:当∠B 是直角时,如图1,△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E=90°,根据“HL”定理,可以知道Rt△ABC≌Rt△DEF.
第二种情况:当∠B 是锐角时,如图2,BC=EF,∠B=∠E<90°,在射线EM上有点D,使DF=AC,画出符合条件的点D,则△ABC和△DEF的关系是 ;
A.全等 B.不全等 C.不一定全等
第三种情况:当∠B是钝角时,如图3,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E>90°.过点C作AB边的垂线交AB延长线于点M;同理过点F作DE边的垂线交DE延长线于N,根据“ASA”,可以知道△CBM≌△FEN,请补全图形,进而证出△ABC≌△DEF.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,直线y=2x﹣2与曲线y= ![]() (x>0)相交于点A(2,n),与x轴、y轴分别交于点B,C.
(x>0)相交于点A(2,n),与x轴、y轴分别交于点B,C.
(1)求曲线的解析式;
(2)试求ABAC的值?
(3)如图2,点E是y轴正半轴上一动点,过点E作直线AC的平行线,分别交x轴于点F,交曲线于点D.是否存在一个常数k,始终满足:DEDF=k?如果存在,请求出这个常数k;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com