为了响应学校提出的“节能减排，低碳生活”的倡议，班会课上小李建议每位同学都践行“双面打印，节约用纸”．他举了一个实际例子：打印一份资料，如果用A4厚型纸单面打印，总质量为400克，将其全部改成双面打印，用纸将减少一半；如果用A4薄型纸双面打印，总质量为160克.已知每页薄型纸比厚型纸轻0.8克，求例子中的A4厚型纸每页的质量.（墨的质量忽略不计）

【题目】如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（﹣2，﹣1）、B（﹣1，1）、C（0，﹣2）．

（1）点B关于坐标原点O对称的点的坐标为；
（2）将△ABC绕点C顺时针旋转90°，画出旋转后得到的△A1B1C；
（3）求过点B1的反比例函数的解析式．

【题目】如图，直线 分别交x轴、y轴于A、B两点，线段AB的垂直平分线分别交x轴、y轴于C、D两点．

（1）求点C的坐标；
（2）求△BCD的面积．

（1）甲、乙两种书柜每个的价格分别是多少元？

（2）若该校计划购进这两种规格的书柜共20个，其中乙种书柜的数量不少于甲种书柜的数量，学校至多能够提供资金4320元，请设计几种购买方案供这个学校选择．

【题目】如图，已知直线，直线和直线交于点C、D,直线上有一点P.

(1)如图1，点P在C、D之间运动时，∠PAC、∠APB、∠PBD之间有什么关系？并说明理由。

(2)若点P在C、D两点外侧运动时(P点与C、D不重合，如图2、3),试直接写出∠PAC、∠APB、∠PBD之间有什么关系，不必写理由。

图1 图2 图3

根据统计图中的信息，解答下列问题：

（）求本次被调查的学生人数．

（）将条形统计图补充完整．

（）若该校共有名学生，请估计全校选择体育类的学生人数．

【题目】如图，在直角坐标系中，O为坐标原点．已知反比例函数y=（k＞0）的图象经过点A（2，m），过点A作AB⊥x轴于点B，且△AOB的面积为．

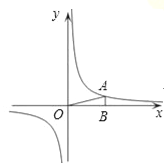
（1）求k和m的值；

（2）点C（x，y）在反比例函数y=的图象上，求当1≤x≤3时函数值y的取值范围；

（3）过原点O的直线l与反比例函数y=的图象交于P、Q两点，试根据图象直接写出线段PQ长度的最小值．

(1)在如图所示的平面直角坐标系画出该四边形；

(2)四边形ABCD的面积是________；

(3)四边形ABCD内（边界点除外)一共有_____个整点(即横坐标和纵坐标都是整数的点).

【题目】如图，直线y=﹣x+b与双曲线 （x＞0）交于A、B两点，与x轴、y轴分别交于E、F两点，连接OA、OB，若S△AOB=S△OBF+S△OAE ， 则b= ．

成证明过程:

∵∠1+∠2=180°( )∠1+∠______=180°

∴∠2=∠DFE( )

∴AB∥EF( )

∴∠3=∠ADE( )

又∵∠3=∠B

∴∠ADE=∠_______

∴DE∥BC( )

∴∠ACB=∠4( ）

∴∠ACB=65°