
科目: 来源: 题型:
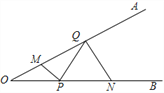
【题目】如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=1,ON=3,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是____________
查看答案和解析>>
科目: 来源: 题型:
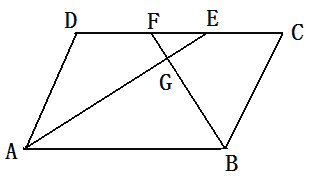
【题目】平行四边形ABCD中, AE、BF分别平分∠DAB和∠ABC交CD于点E、F.AE、BF交于点G.
(1)求证AE⊥BF
(2)判断DE和CF的大小关系,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场计划拨款9万元从厂家购进50台电视机,已知该厂家生产三种不同型号的电视机,出厂价分别为:甲种每台1500元,乙种每台2100元,丙种每台2500元,若商场同时购进其中两种不同型号电视机共50台,用去9万元,请你研究一下商场的进货方案.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣3交y轴于点C,直线l为抛物线的对称轴,点P在第三象限且为抛物线的顶点.P到x轴的距离为 ![]() ,到y轴的距离为1.点C关于直线l的对称点为A,连接AC交直线l于B.
,到y轴的距离为1.点C关于直线l的对称点为A,连接AC交直线l于B. 
(1)求抛物线的表达式;
(2)直线y= ![]() x+m与抛物线在第一象限内交于点D,与y轴交于点F,连接BD交y轴于点E,且DE:BE=4:1.求直线y=
x+m与抛物线在第一象限内交于点D,与y轴交于点F,连接BD交y轴于点E,且DE:BE=4:1.求直线y= ![]() x+m的表达式;
x+m的表达式;
(3)若N为平面直角坐标系内的点,在直线y= ![]() x+m上是否存在点M,使得以点O、F、M、N为顶点的四边形是菱形?若存在,直接写出点M的坐标;若不存在,请说明理由.
x+m上是否存在点M,使得以点O、F、M、N为顶点的四边形是菱形?若存在,直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合).以AD为边作正方形ADEF,连接CF.
(1)如图1,当点D在线段BC上时,求证:①BD⊥CF.②CF=BC﹣CD.
(2)如图2,当点D在线段BC的延长线上时,其它条件不变,请直接写出CF、BC、CD三条线段之间的关系;
(3)如图3,当点D在线段BC的反向延长线上时,且点A、F分别在直线BC的两侧,其它条件不变:①请直接写出CF、BC、CD三条线段之间的关系.②若连接正方形对角线AE、DF,交点为O,连接OC,探究△AOC的形状,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过D作直线DE垂直BC于F,且交BA的延长线于点E.
(1)求证:直线DE是⊙O的切线;
(2)若cos∠BAC= ![]() ,⊙O的半径为6,求线段CD的长.
,⊙O的半径为6,求线段CD的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,大楼AB高16米,远处有一塔CD,某人在楼底B处测得塔顶的仰角为38.5°,爬到楼顶A处测得塔顶的仰角为22°,求塔高CD及大楼与塔之间的距离BD的长.(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin38.5°≈0.62,cos38.5°≈0.78,tan38.5°≈0.80 )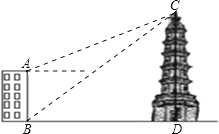
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com