
科目: 来源: 题型:
【题目】阅读下面材料:
如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2= ![]() 交于A(1,3)和B(﹣3,﹣1)两点.
交于A(1,3)和B(﹣3,﹣1)两点.
观察图象可知:
①当x=﹣3或1时,y1=y2;
②当﹣3<x<0或x>1时,y1>y2 , 即通过观察函数的图象,可以得到不等式ax+b> ![]() 的解集.
的解集.
有这样一个问题:求不等式x3+4x2﹣x﹣4>0的解集.
某同学根据学习以上知识的经验,对求不等式x3+4x2﹣x﹣4>0的解集进行了探究.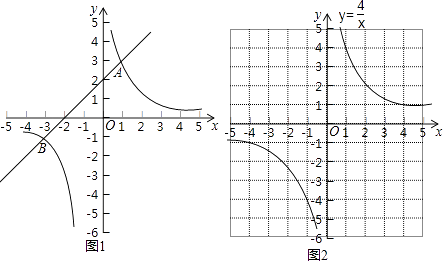
下面是他的探究过程,请将(2)、(3)、(4)补充完整:
(1)将不等式按条件进行转化:
(2)构造函数,画出图象
设y3=x2+4x﹣1,y4= ![]() ,在同一坐标系中分别画出这两个函数的图象.
,在同一坐标系中分别画出这两个函数的图象.
双曲线y4= ![]() 如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
(3)确定两个函数图象公共点的横坐标,观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足y3=y4的所有x的值为
(4)借助图象,写出解集
结合(1)的讨论结果,观察两个函数的图象可知:不等式x3+4x2﹣x﹣4>0的解集
查看答案和解析>>
科目: 来源: 题型:
【题目】计算
(1)5.6+(﹣0.9)+4.4+(﹣8.1)+(﹣0.1)
(2)5+(﹣![]() )﹣7﹣(﹣2.5)
)﹣7﹣(﹣2.5)
(3)(﹣![]() )×(﹣
)×(﹣![]() )+(﹣
)+(﹣![]() )×(+
)×(+![]() )
)
(4)![]()
(5)8﹣23÷(﹣4)3+![]()
(6)(﹣1)2018+(﹣5)×[(﹣2)3+2]﹣(﹣4)2÷(﹣![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为

A.![]() B.3 C.1 D.
B.3 C.1 D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】下列说法正确的是_____(填写符合要求的序号)
(1)两个有理数的和为负数时,这两个数都是负数;
(2)如果两个数的差是正数,那么这两个数都是正数;
(3)几个有理数相乘,当负因数个数为奇数时,乘积一定为负;
(4)数轴上到原点的距离为3的点表示的数是3或﹣3;
(5)0乘以任何数都是0.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,为美化校园环境,某校计划在一块长为100米,宽为60米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米﹒
(1)用含a的式子表示花圃的面积;
(2)如果通道所占面积是整个长方形空地面积的![]() ,求出此时通道的宽;
,求出此时通道的宽;
(3)已知某园林公司修建通道的单价是50元/米2,修建花圃的造价y(元)与花圃的修建面积S(m2)之间的函数关系如图2所示,并且通道宽a(米)的值能使关于x的方程![]() x2-ax+25a-150有两个相等的实根,并要求修建的通道的宽度不少于5米且不超过12米,如果学校决定由该公司承建此项目,请求出修建的通道和花圃的造价和为多少元?
x2-ax+25a-150有两个相等的实根,并要求修建的通道的宽度不少于5米且不超过12米,如果学校决定由该公司承建此项目,请求出修建的通道和花圃的造价和为多少元?

查看答案和解析>>
科目: 来源: 题型:
【题目】某学校刚完成一批结构相同的学生宿舍的修建,这些宿舍地板需要铺瓷砖,一天4名一级技工去铺4个宿舍,结果还剩12 m2地面未铺瓷砖;同样时间内6名二级技工铺4个宿舍刚好完成,已知每名一级技工比二级技工一天多铺3 m2瓷砖.
(1)求每个宿舍需要铺瓷砖的地板面积.
(2)现该学校有20个宿舍的地板和36 m2的走廊需要铺瓷砖,某工程队有4名一级技工和6名二级技工,一开始有4名一级技工来铺瓷砖,3天后,学校根据实际情况要求2天后必须完成剩余的任务,所以决定加入一批二级技工一起工作,问需要再安排多少名二级技工才能按时完成任务
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC. 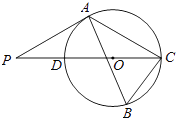
(1)求证:PA是⊙O的切线;
(2)若AB=4+ ![]() ,BC=2
,BC=2 ![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,两直线AB,CD相交于点O,已知OE平分∠BOD,且∠AOC:∠AOD=3:7,

(1)求∠DOE的度数;
(2)若OF⊥OE,求∠COF的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线AB:y=5x﹣5与x轴交于点A,与y轴交于点B,点C与点B关于原点O对称,抛物线y=ax2+bx+c的对称轴为直线x=3且过点A和C. 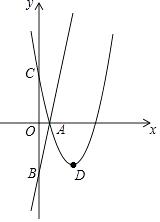
(1)求点A和点C的坐标;
(2)求抛物线y=ax2+bx+c的解析式;
(3)若抛物线y=ax2+bx+c的顶点为D,且在x轴上存在点P使得△DAP的面积为6,直接写出满足条件的点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
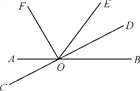
【题目】如图,直线AB与CD相交于点O,OF,OD分别是∠AOE,∠BOE的平分线.
(1)写出∠DOE的补角;
(2)若∠BOE=62°,求∠AOD和∠EOF的度数;
(3)试问射线OD与OF之间有什么特殊的位置关系?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com