
科目: 来源: 题型:
【题目】如图(1)是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状.抛物线两端点与水面的距离都是1m,拱桥的跨度为10cm.桥洞与水面的最大距离是5m.桥洞两侧壁上各有一盏距离水面4m的景观灯.现把拱桥的截面图放在平面直角坐标系中,如图(2).求: 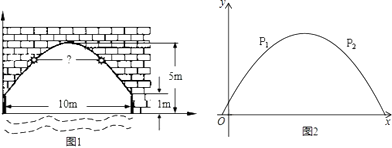
(1)抛物线的解析式;
(2)两盏景观灯P1、P2之间的水平距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平整的地面上,由若干个完全相同的棱长为 10 cm 的小正方体堆成一个几何体,如图 所示.
(1)这个几何体由多少个小正方体组成?请画出这个几何体的三视图.
(2)如果在这个几何体的表面(不包括底面)喷上黄色的漆,则在所有的小正方体中,有多少个只有一个面是黄色?有多少个只有两个面是黄色?有多少个只有三个面是黄色?
(3)假设现在你手里还有一些相同的小正方体,保持这个几何体的主视图、俯视图形状 不变,最多可以再添加几个小正方体?这时如果要重新给这个几何体表面(不包括底面) 喷上红色的漆,需要喷漆的面积比原几何体增加了还是减少了?增加或减少的面积是 多少?

查看答案和解析>>
科目: 来源: 题型:
【题目】有一种牛奶软包装盒如图1所示.为了生产这种包装盒,需要先画出展开图纸样.
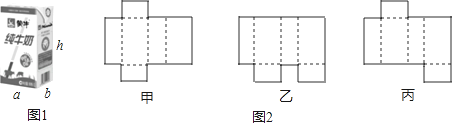
(1)如图2给出三种纸样甲.乙.丙,在甲.乙.丙中,正确的有________.
(2)从已知正确的纸样中选出一种,在原图上标注上尺寸.
(3)利用你所选的一种纸样,求出包装盒的侧面积和表面积(侧面积与两个底面积的和)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,从图 2 开始,每一个图形都是由基本图形“△”通过平移或翻折拼成的:

观察发现,图 10 中共有_________________个小三角形,图 n 共有____________个小三角形,
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在一次数学活动课上,张明用17个边长为1的小正方形搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要 个小立方体,王亮所搭几何体的表面积为 .

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形ABCD的边长为2,E是BC的中点,以点A为中心,把△ABE逆时针旋转90°,设点E的对应点为F. 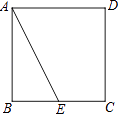
(1)画出旋转后的三角形.
(2)在(1)的条件下,
①求EF的长;
②求点E经过的路径弧EF的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:

(1)小明总共剪开了_______条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:二次函数y=﹣x2+bx+c的图象过点(﹣1,﹣8),(0,﹣3).
(1)求此二次函数的表达式,并用配方法将其化为y=a(x﹣h)2+k的形式;
(2)用五点法画出此函数图象的示意图. 
查看答案和解析>>
科目: 来源: 题型:
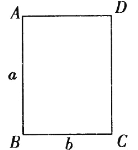
【题目】如图,长方形 ABCD 中, AB = a, BC = b, a > b .以 AB 边为轴将长方形旋转一周形成 圆柱体甲,再以 BC 边为轴将长方形旋转一周形成圆柱体乙.记两个圆柱体的体积分别为 V甲 ,V乙 ,侧面积分别为 S甲, S乙 ,则下列正确的是( )
A. V甲 > V乙 , S甲=S乙
B. V甲 < V乙 , S甲= S乙
C. V甲= V乙 , S甲= S乙
D. V甲 > V乙 , S甲 < S乙
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com